Windenergie 1 - Strukturdynamik

05 June 2025, Po Wen Cheng

Motivation: Warum Dynamische Berechnungen?

• Warum reichen statische Berechnungen nicht aus?
• Rotorblatt als *linear und starrer Balken, einseitig fest eingespannt

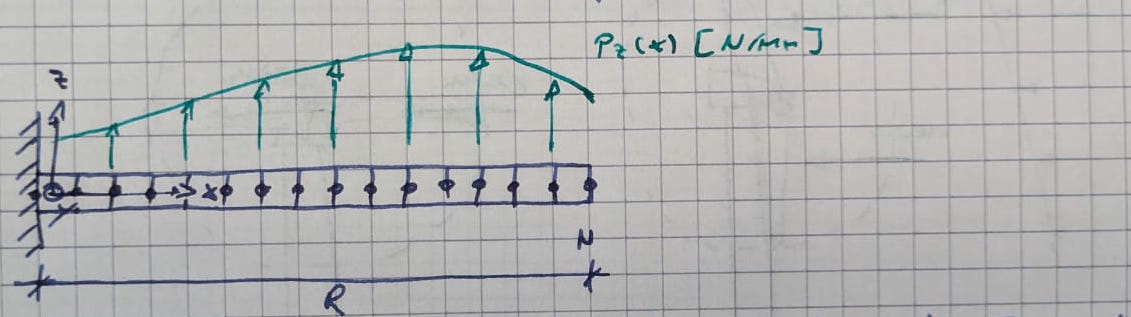
• Aerodynamische Kräfte, Gewichtskräfte als statische Streckenlast (keine Funktion der Zeit)
• Schnittlasten bestimmen mit Kräfte- und Momentengleichgewicht
• Statische Berechnungen sind brauchbar für grobe Abschätzungen aber nicht für Strukturauslegung

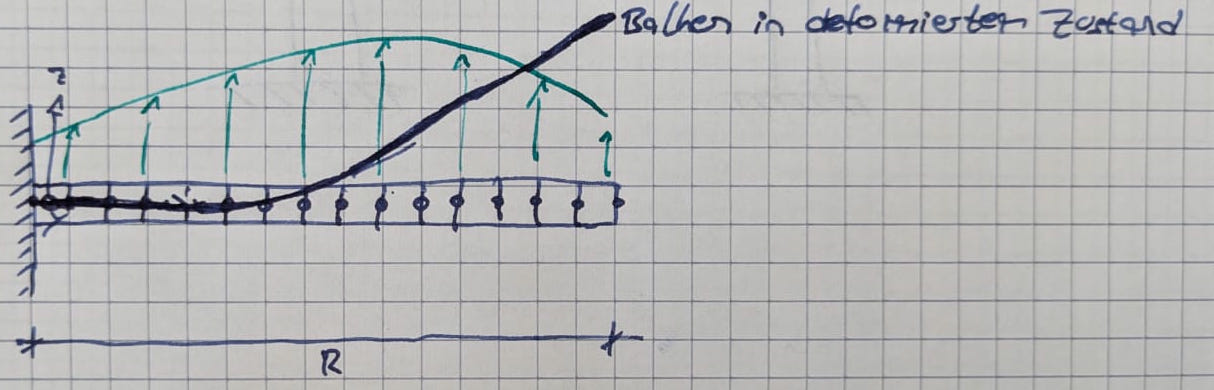
• Rotorblatt als flexibler Balken, einseitig festeingespannt
• Aerodynamische Kräfte, Gewichtskräfte als dynamische Streckenlast (eine Funktion der Zeit)
• Schnittlasten bestimmen mit der Lösung der Bewegungsdifferentialgleichung
• Dynamische Berechnungen sind notwendig für Strukturauslegung, berücksichtigt die dynamische Amplifikation
• Die Strukturdeformation kann bestimmt werden

Koordinatensysteme

Verwendung von drei Koordinatensystemen um die Belastungsgrößen darzustellen

1. KS im Rotorblattquerschnitt
2. KS im Rotormittelpunkt (Nabe)
3. KS im Turmfuß

KS basiert auf Konvention. Unterschiedliche Programme verwenden unterschiedliche KS - Daher immer überprüfen

Raumfeste KS vs. drehendes KS (Gierwinkel, Azimuthwinkel, Pitchwinkel)

Typische Auslegungslasten für Windenergieanlagen

• Schwenk- und Schlagmoment in Rotorblatt Blattkoordinatensystem
• Drehmoment, In-Plane und Out-of-Plane Biegemomente in Nabenkoordinatensystem
• Schubkraft, Nick-, Roll- und Giermoment in Turmkopfkoordinatensystem

Anregung durch atmosphärische Turbulenz

• Kurzzeitige, lokale Änderung des Windrichtungs- und Windgeschwindigkeitsvektors
• Thermische und mechanische (Rauhigkeits-) Einflüsse
  • Zeitliche und räumliche Turbulenzstrukturen

Dynamische Anregungen: Einteilung von Belastungen

Lasten können je nach KS konstand oder zeitlich veränderlich sein - Schwerkraft des Turms Konstant, Schwerkraft eines Blatts verursacht aber periodische Lasten für das Blatt

Dynamische Lasten werden durch Regelung und Betrieb der Analge beeinflusst (Rotorblatt pitchen, Windnachführung, ...)

Externlasten

• Luftkräfte bei gleichförmiger, stationärer Rotoranströmung
• Periodisch wechselnde Luftkräfte
• Stochastische Luftkräfte durch Wirbelturbulenz
• Stochaastische Wellenkräfte auf Gründungsstruktur

Internlasten

• Massenkräfte
  • Gewichtskräfte
  • Zentrifugalkräfte
  • Kreiselkräfte
  • Massenumwucht

Bewegungsgleichung elastischer Strukturen

$$M \ddot{q} + B \dot{q} + K q = F(t)$$

$M$: Masse
$D$: Dämpfung
$S$: Federsteifigkeit
$F(t): Anregungskraft
$q$: Generalisierte Koordinate

Stationäre Lasten aus Wind- und Massenkräften

• Eigengewicht
• Stationäre Luftkräfte aus mittlerer Windgeschwindigkeit (Abhängigkeit der Lasten von der Windgeschwindigkeit hängen vom Anlagenkonzept Pitch / Stall ab)

Periodosche und transiente Lasten aus Massenkräften

• Massenkräfte durch Eigengewicht
• Kreisel- und Corioliskräfte bei Manövern
• Massenumwucht

Transformation der Rotorblattlasten auf die Gondel

• Blattwurzelbiegemomente infolge von
  • Eigengewicht, Transformation in ein Rollmoment
  • Fliehkräfte, Transformation in ein Rollmoment

Drei Blatt Rotor ideal in Bezug auf Reduktion der wirkenden Kräfte durch symmetrie und in Bezug auf Produktionskosten (Im Gegensatz zu vier Blättern)

Superposition von Blatt-Lasten, Bsp. Höhenprofil

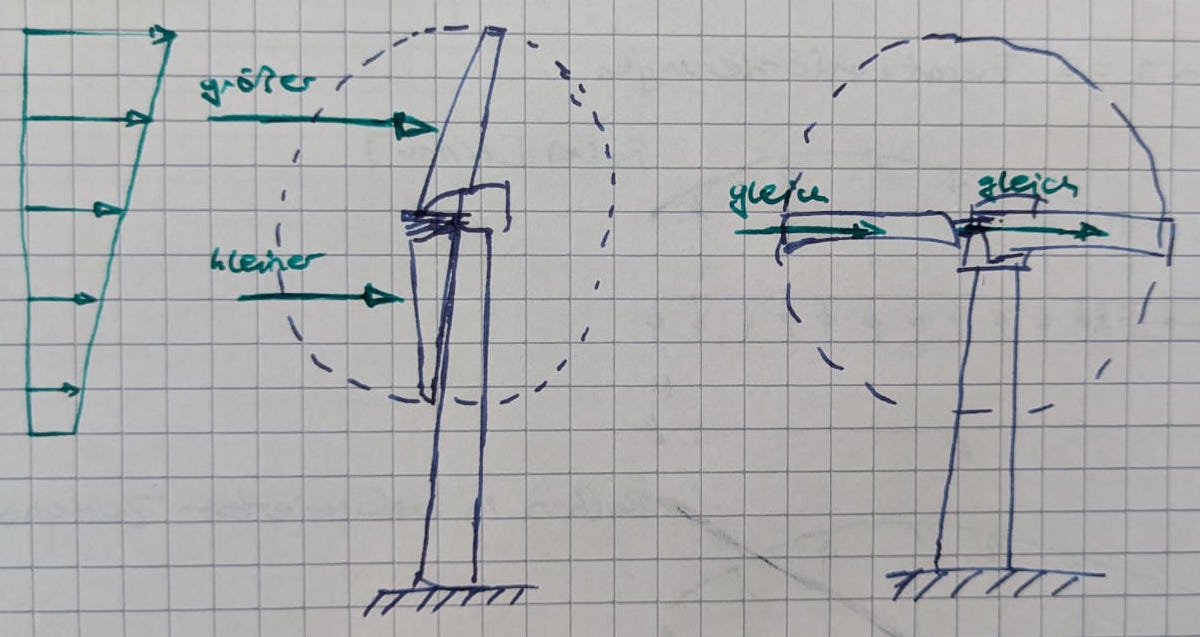
• Keine Auslöschung der Wechsellasten (im Gegensatz zum drei Blatt Rotor)
• effektiver Druckpunkt verschiebt sich auf und nieder
• Gondel Nickmoment variiert mit 2P
• Welle 1P-Wechsellast