Windenergie 1 - Aerodynamik 1

08 May 2025, Christian Molter

Energiefluss bei der Windenergienutzung

Sonnenenergie - Wind-Strömungsenergie - mechanische Rotationsenergie durch Abbremsung mit dem Windrotor - Elektrische Energie - Transport über Hochspannungsleitung - Verbrauch als Niederspannung

Energie und Leistung des Windes

Kinetische Energie des Windes: $E = \frac{1}{2} m v_1^2$
Massendurchsatz $\dot{m} = F \rho v_1$
Leistung des Windes $P_wind = \dot{E} = \frac{1}{2} \dot{m} v_1^2 = \frac{1}{2} F \rho v_1^3$
Leistung des Windes ist proportional zur Dritten Potenz der Windgeschwindigkeit

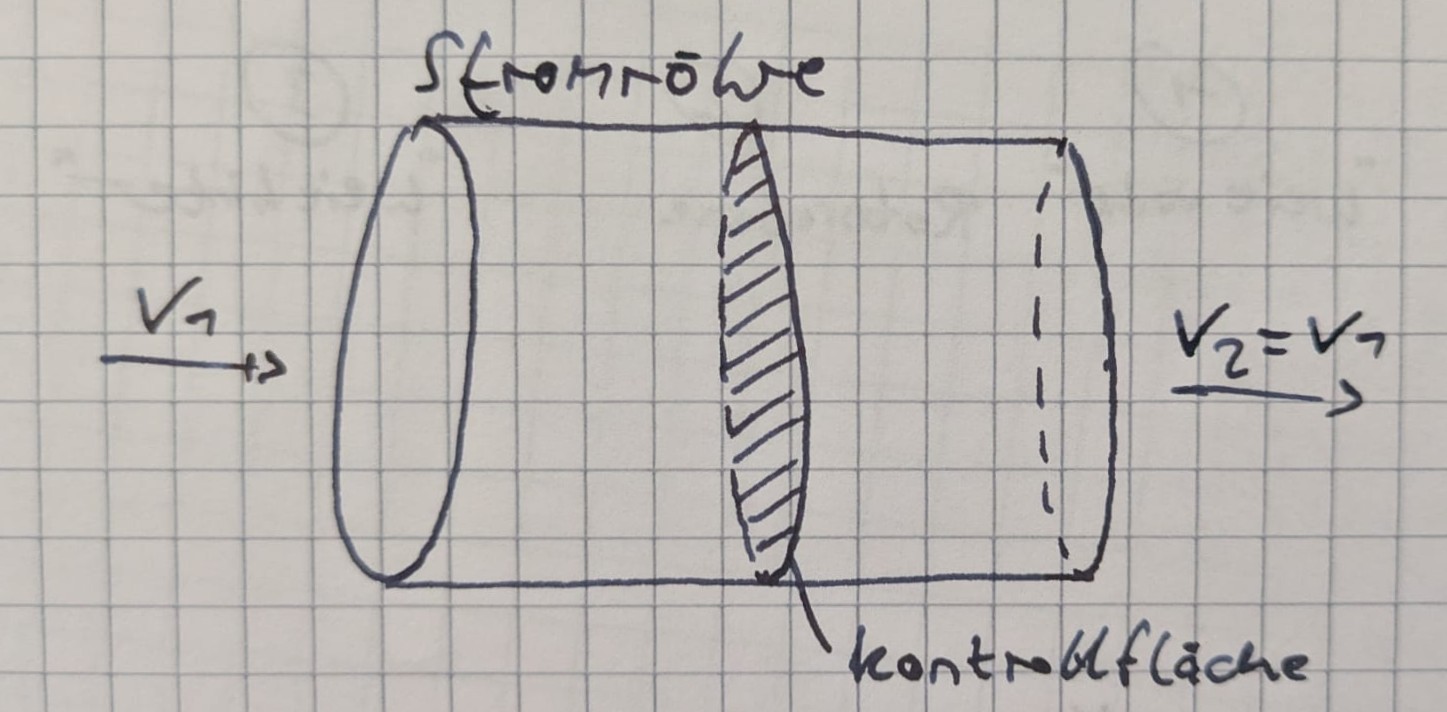
Energieentnahme durch Abbremsung

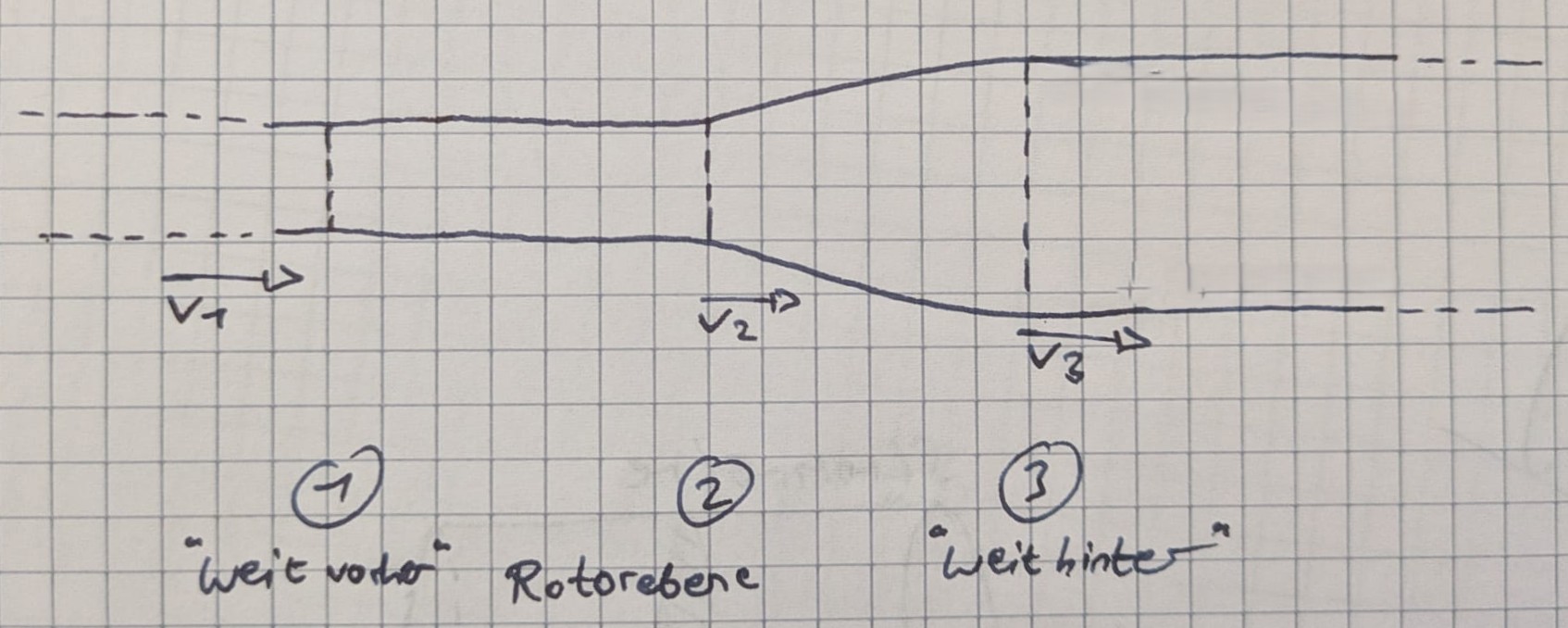
• Energieentnahme durch "irgendeine" Art von Konverter bewirkt kontinuierliche Abbremsung der Geschwindigkeit von $v_1$ weit davor über $v_2$ im Konverter zu $v_3$ weit dahinter
• Kontinuitätsbedingung (konstanter Massenstrom) $\rightarrow$ Aufweitung der Stromröhre durch Abbremsung\ $\rho v_1 F_1 = \rho v_2 F_2 = \rho v_3 F_3$
• keine Energieentnahme ohne oder bei vollständiger Abbremsung (Luft muuss durch Konverter Strömen)

Nutzleistung im Konverter $P$ kann sowohl aus dem Impulssatz als auch aus der Energiebilanz berechnet werden

Windgeschwindigkeit im Konverter: $v_2 = \frac{(v_1+v_3)}{2}$

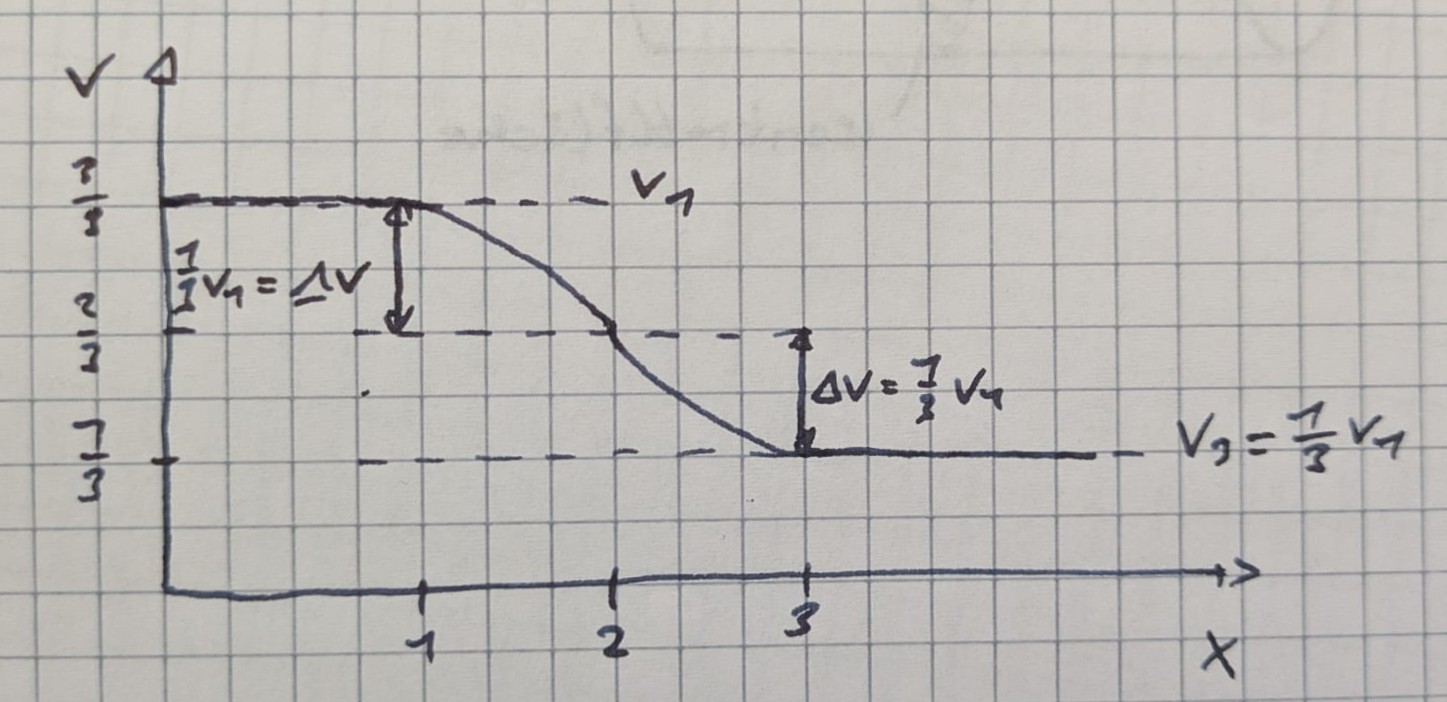
Im günstigsten Fall der völlig verlustfrei angenommenen Leistungsentnahme sind nur 59% der Windleistung mechanisch nutzbar

ACtuator-Disc-Modell

Keine Rotorblätter, sondern einfache Scheibe die die Strömung abbremst, also keine Verwirbelungen etc.
Betz-Optimum $a = \frac{1}{3}; \qquad c_s = \frac{8}{9} \qquad c_p = \frac{16}{27}$

Schub = Schubbeiwert $\cdot$ Staudruck $\cdot$ Rotorfläche

Bei optimaler Abbremsung ist die Schubkraft auf die Rotorblätter ähnlich groß wie die fiktive Widerstandkraft der als geschlossen angenommen überstrichenen Rotorfläche

Dimensionslose Kenngrößen und Kennlinien

Vorteile:

• Unabhängig von Dimensionen und Einheiten
• Verminderung der Anzahl der Parameter

Wichtige Dimensionslose Größen:

• Schnelllaufzahl $\lambda$
• Leistungsbeiwert $c_P$, Schubbeiwert $c_S$, Momentenbeiwert $c_M$
• Induktionsfaktoren $a, a`$
• Auftriebsbeiwert $c_a$ und Widerstandsbeiwert $c_w$

Rotoren gleicher Schnelllaufzahl verhalten sich aerodynamisch ähnlich (solange Reynolds-Effekte vernachlässigbar)

Fazit

• Windleistung proportional zu dritten Potenz der Windgeschwindigkeit
• optimale Abbremsung weit hinter dem Konverter auf $\frac{v_1}{3}$
• maximaler aerodynamischer Wirkungsgrad nach Betz $\approx$ 59%
• Actuator-Disk-Modell (ohne Rotation des Nachlaufs)
• induzierte Geschwindigkeit i.d. Rotorebene $v_i = a v_1$
• Induktionsfaktor $a$
• Schub- und Leistungsbeiwert $c_S = f a; \qquad c_P = f a$
• Dimensionslose Kenngrößen
• Verhalten eines typischen Schnellläufers anhand der dimensionslosen Kennlinien $c_P$, $c_M$ und $c_S$ über $\lambda$