Windenergie 1 - Wind 2
24 April 2025, Po Wen Cheng
Berechnung des Energieertrags einer Windenergieanlage
Was wird benötigt?
- Standort
- Histogramm oder (Weibull- oder Rayleigh-) Verteilung der Windgeschwindigkeit (gemittelt über 10 min)
- Windenergieanlage
- Leistungskurve - Welche Leistung gibt die Anlage bei welcher Windgeschwindigkeit ab
- Standort und Anlage
- Brutto - Jahres - Energieertrag
- Multiplikation der Windstunden mit dem Energiebetrag - [kWh]
Annahme: Turbulenz ist Gaußisch - Normalverteilt. Eine Statistik der Windgeschwindigkeitsschwankungen ergibt eine Gaußsche Verteilung der Geschwindigkeiten um einen Mittelwert herum.
Langzeitstatistik (ein oder meherere Jahre):
- $v_m$ (Jahres-) Mittel der Windgeschwindigkeit
- Verteilungsdichtefunktion der mittleren Windgeschwindigkeit $f(v)$
- Windrichtungsverteilung
- Höhengradient
Kurzzeitstatistik (Mitteilungszeitraum 10 min bis 1 h):
- mittlere Windgeschwindigkeit $\overline{v}$ d.h. im Allgemeinen der 10 min Mittelwert der momentanen Eindgeschwindigkeit $v(t)$
- Turbulenzintensität $I_T$ [%] d.h. Verhältnis der Standartabweichung $\sigma$ der Windgeschwindigkeit $v(t)$ zur mittleren Windgeschwindigkeit $\overline{v}$
- Windrichtung, Hähengradient, ggfs. Stabilitätsbedingungen (Schichtung)
Histogramm und Häufigkeitsverteilung
kumulative Häufigkeitsverteilung, Summenhäufigkeit (Folie 13)
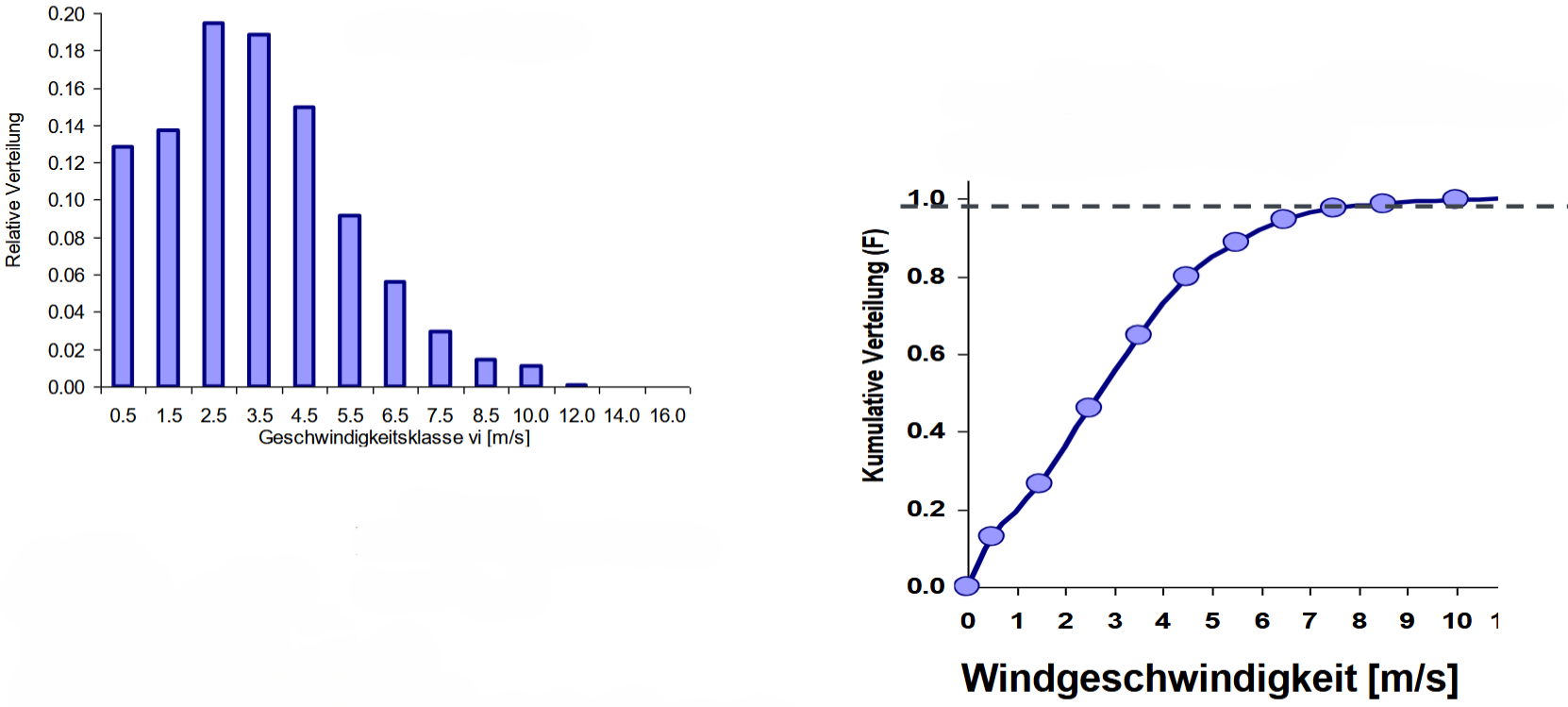
bei z.B. einer Windgeschwindigkeit von $10 \frac{m}{s}$ und einer Kumulativen Verteilung $F = 0,3$: Es gibt eine 30% Wahrscheinlichkeit, das die Windgeschwindigkeit kleiner sein wird als $10 \frac{m}{s}$
Verteilungsdichtefunktion:
$$f(v) = \frac{k}{A} (\frac{v}{A})^{k-1} \cdot exp[-(\frac{v}{A})^k]$$
Kumulative Verteilung
$$F(v) = 1-exp[-(\frac{v}{A})^k]$$
Weibullfaktoren:
Skalierungsparameter $A$ [$\frac{m}{s}$], proportional zu $v_m$
Formfaktor $k$ [-] (hier $1 < k < 4$)
Zusammenhang zwischen Weibullfaktoren $A$ und $k$ und dem Jahresmittel $v_m$ der Windgeschwindigkeit
$$v_m \approx A \cdot (0.568 + \frac{0.434}{k})^{1/k}$$
Vertikale Hüchrechnung der Weibull-Verteilung
Vereinfachende Annahme: $k_2 = k_1$ (Formfaktor ist in beiden Höhen gleich)
logarithmisches Windprofil
$$A_2 = A_1 \frac{\ln(z_2/z_0)}{\ln(z_2/z_0)}$$
Rayleigh-Verteilung ist ungefär Weibull-Verteilung für $k = 2$ (europäischer Standort) $\rightarrow$ Daher nur noch eine Variable (Siehe Folie 17)
Weibull-Verteilung ist ungenau für extrapolation von hohen Windgeschwindigkeiten / Extremsituationen
Jährliche Schwankungen des Windangebots gegenüber eine langjährigen Mittelung
- Windjahrt = (1 - Energieertrag / Referenz) einer fiktiven Eindenergieanlage im Vergleich zum langjährigen Mittel
- Energiegehalt des Windes kann bis zu $\pm$ 25% pro Jahr schwanken
- Je nach Klimazone starke jahreszeitliche Schwankungen
Beispiel Leistungskurve einer WEA
"Das ist sehr wichtig dass sie das können"
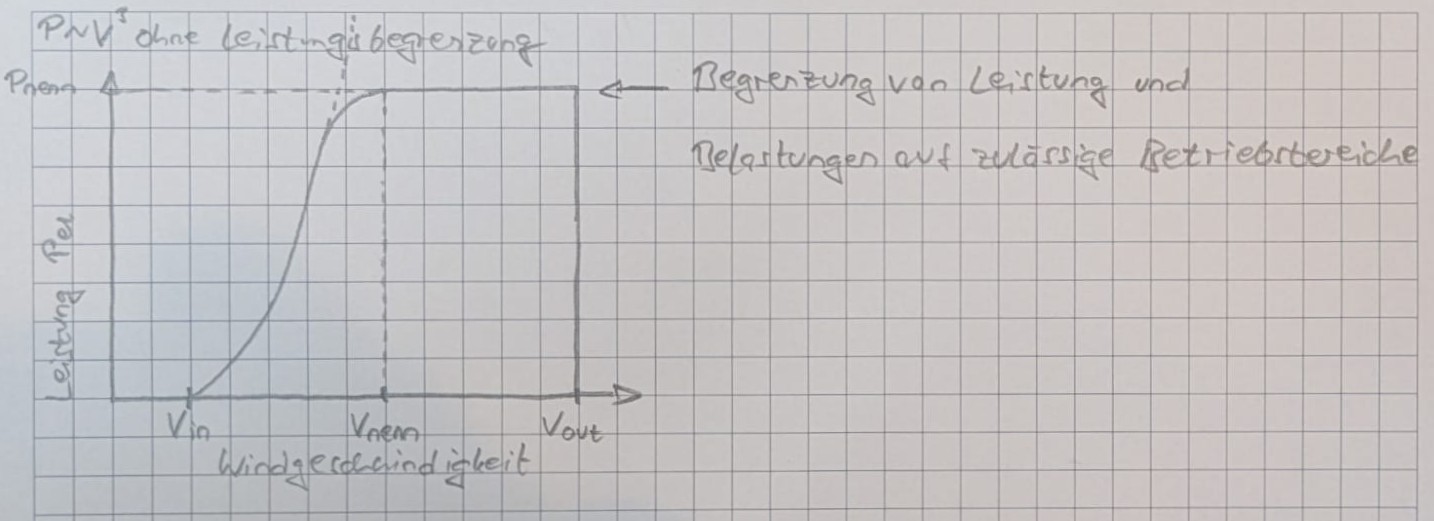
$V_{in} = ca. 3.5 - 4 \frac{m}{s}$
Einschaltgeschwindigkeit (Beginn positiver Leistungsproduktion)
$V_{nenn} = ca. 11 - 12 \frac{m}{s}$
Nenngeschwindigkeit (Nennleistung wird erreicht)
$V_{out} = ca. 25 \frac{m}{s}$
Abschaltgeschwindigkeit (Produktionsstopp, Anlage trudelt)