Einführung in die Verbrennung - Vorlesung

05 June 2025, Andreas Huber, Torsten Methling, Holger Huck, Nils Jakobs

Grundlagen der Reaktionskinetik / Chemischen Kinetik

Grob: Die Glwischenschritte

Detailliert: Während eines Reaktionsverlaufs finden viele Zwischenschritte statt, die durch Elementarreaktionen abgebildet werden

Charakteristische Größen:

• Adiabatische Flammentemperatur steigt bei der Verbrennung
• Dichte sinkt
• Geschwindigkeit steigt (Massenfluss muss gleich bleiben - Massenerhaltung)

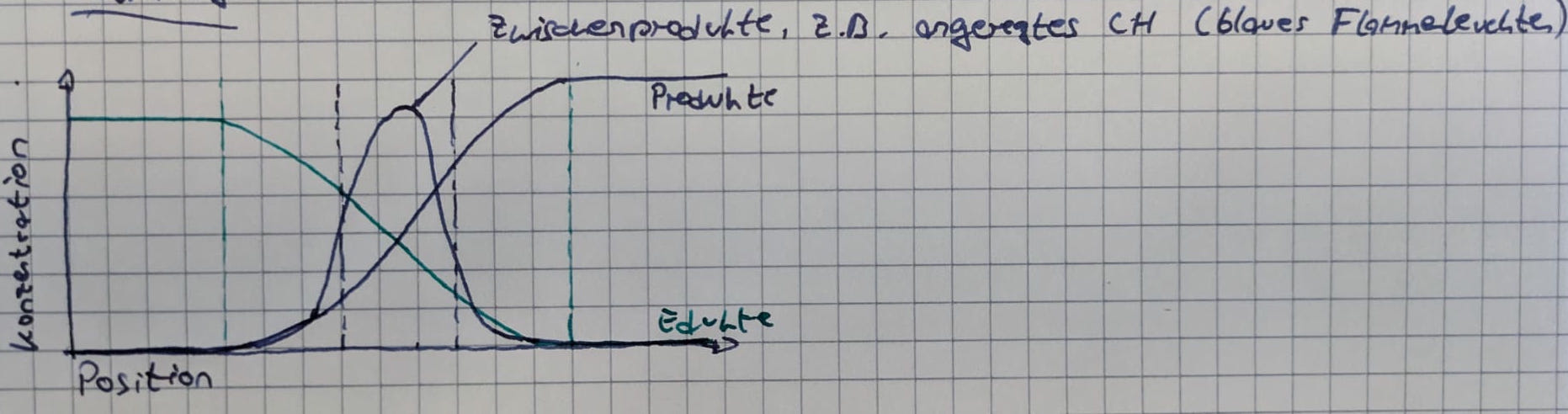
Die Flamme aus kinetischer Sicht

• T steigt in der Vorheizzone aufgrund von Wärmeleitung, danach weiter bis nach der Hauptreaktionszone die Flammentemperatur T erreicht wird.
• Hauptreaktionszone wird als Flamme bezeichnet
• Der Brennstoff reagiert mit dem Oxidator unter Bildung zahlreicher Zwischenprodukte zu den Verbrennungsendprodukten wie Wasser und CO2
• Alle reagierenden Teilchen bezeichnet man zusammenfassend als chemische Spezies

Kinetik und Thermoddynamik

Gesetze der Thermodynamik können nicht das Gleichgewicht der Verbrennungsprodukte und der Maximaltemperatur bestimmen - Dies hängt von Zeitskalen ab

Bsp: Gleichgewichtseinstellung Methan / Luft bei 1400 K:
Thermodynamisches Gleichgewicht erreicht erst nach ca. 7 ms
Vorher: Zeitabhängige kinetische Prozesse
Zeitskalen hängen von verschiedenen Bedinungen ab:

• Magere Verbrennung
• Stöchometrische Verbrennung
• Fette Verbrennung

Definition

Chemische Kinetik ist die Untersuchung von Geschwindigkeiten chemischer Reaktionen und der Schritte, nach denen diese verlaufen

Bedeutung chemischer Kinetik:

• Beschreibt Zündprozesse, Flammenausbreitung und Schadstoffbildung
• Essenziell für sicheren und zuverlässigen Betrieb von Verbrennungssystemen mit niedrigen Schadstoffemissionen

Chemisch - kinetisches Reaktionmodell: Bestandteile

• Reaktionsmechanismus
• Thermodynamische Daten:
  • Wärmekapazität, Enthalpie, Entropie
  • Energieerhaltung
  • Reaktionsgeschwindigkeit Rückreaktion
• Stoffspezifische Größen zur Bestimmung des Stofftransports (z.B. Diffusion)

Reaktionsmechanismus

Bildet alle relevanten Reaktionsschritte und Spezies eines Verbrennungssystems ab, Relevanz abhängig von Anwendungsziel
Reaktionsschritte können über Globalreaktionen oder Elementarreaktionen abgebildet werden

Grund dass es beides gibt, ist der Rechenaufwand: Rechenaufwand in der CFD skaliert kubisch mit Anzahl der Spezies

Wann ist eine Reaktion eine Elementarreaktion?

• Nicht wenn:
  • Summe der stöchiometrischen Koeffizienten > 3
  • Beispiel: $C_2H_4 + 3 O_2 \rightleftarrows CO_2 + 2 H_2O$
  • Nicht ganzzahlige stöchiometrische Koeffizienten
• Was wenn:
  • Summe der stöchiometrischen Koeffizienten < 3
    • Aufklärung nur über experimentelle oder numerische Untersuchungen
    • Kann nicht nur anhand der Reaktionsgleichung entschieden werden

Reaktionsgeschwindigkeit

Zeitgesetz: Empirischer Ansatz für die Bildung oder Verbrauch einer an der Reaktion beteiligten Spezies mit der Reaktionsgeschwindigkeit: (Eckige Klammer steht für Einheit)

$$\frac{d[A]}{dt} = -k[A]^a [B]^b [C]^c ...$$

• Reaktionsordnung bzgl. A ist a
• Gesamtreaktionsordnung: $a+b+c+...$
• k Geschwindigkeitskoeffizient (Funktion von T teilweise von p)

Bei Elementarreaktionen entspricht die Reaktionsordnung einer Spezies ihrem Stöchiometriefaktor $v_i$

Bei Globalreaktionen gilt:
die Reaktionsordnung einer Spezies i wird für einen definierten Bereich (z.B. $T, p, \lambda$) so gewählt, dass die Spezies möglichst ähnlich zur Realität gebildet und abgebaut werden (Gültigkeit / Genauigkeit eingeschränkt)

Anwendung: Grobe Verbrennungsbeschreibung bei geringer Rechenleistung

Typen von Elementarreaktionen

• Unimolekulare Reaktion
  • A $\rightarrow$ Produkte
• Bimolekulare Reaktion
  • A + B $\rightarrow$ Produkte
• Trimolekulare Reaktion
  • A + B + C $\rightarrow$ Produkte

Integrierte Zeitgesetze

• Zeitgesetz beschreibt die Konzentrationsänderung
  • Differenzialgleichung $\frac{d[A]}{dt} = -k f([A], [B], \dots)$
• Integriertes Zeitgesetz: Lösung dieser Differentialgleichung
• Nutzen
  • Bekannte Reaktionsordnung: Konzentration aus Funktion der Zeit kann bestimmt werden
  • Unbekannte Reaktionsordnung: Integr. Zeitgesetz kann zur Bestimmung der Reaktionsordnung genutzt werden
  • Bekannte Reaktionsordnung, bekannte Konzentrationsverläufe: Bestimmung von $k$

Reaktionskoeffizient $k$

• Bisher: k als bekannt / konstant angenommen
• Jetzt: $k = k(T)$
• Empirischer Befund:
  • k hängt stark und nichtlinear von T ab
  • Nimmt zu wenn T steigt
  • Arrheniusgleichung

Temperaturabhängigkeit von $k$

$$k = A exp(-\frac{E_A}{R_m T})$$

$A$: Frequenzfaktor (=Anzahl von Zusammenstöße pro Zeiteinheit)
$E_A$: Aktivierungsenergie

$E_A$ entspricht einer Energieschwelle, die beim Ablauf der Reaktion zu überwinden ist
Maximaler Wert: Wert der beteiligten Bindungsenergien

Werden neue Bindungen gebildet, kann sich die Aktivierungsenergie bis auf 0 vermindern
Vorwärts und Rückwärtsreaktionen haben verschiedene $E_A$

Physikalische Interpretation:

• $E_A$ Aktivierungsenergie
• $A$ Frequenzfaktor
• Bimolekulare Reaktion: $A$ gibt an, wie häufig zwei Teilchen zusammenstoßen
• $exp(-\frac{E_A}{R_m T})$ ist der Bruchteil der Teilchen, der die zur Reaktion notwendigen Energie besitzt "Boltzmannfaktor"
• Tatsächliche k-Werte kleiner: Orientierung der Moleküle
• A groß bei A groß, T hoch, $E_A$ niedrig

Aus Messungen ableitbar: Schwache Temperaturabhängigkeit des präexponentiellen Faktors $A$ - Erweiterung:

$$k = A' T^b exp(-\frac{E'_A}{R_m T})$$

Druckabhängigkeit von $k$

• In der Regel gilt Arrhenius-Ansatz $k = k(T)$
• Zusätzlich gibt es druckabhängige Reaktionsgeschwindigkeitskoeffizienten $k(T,p)$

Lindemann Modell der Druckabhängigkeit:

• Modellvorstellung
  • Zerfallsreaktion kann nur stattfinden, wenn das Molekül einen angeregten Zwischenzustand mit hoher Energie erreicht
  • Diese Energie wird zugeführt durch Stoß mit einem anderen Teilchen