Turboflugtriebwerke - Verdichter

28 April 2025, Stephan Staudacher

Der Geschwindigkeitskoeffizient

$$C_{v9} = \frac{w_{9,real}}{w_{9,ideal}} \leq 1$$

Der Geschwindigkeitskoeffizienz ist nicht direkt messbar, da eine präzise Erfassung des Geschwindigkeitsfeldes in Ebene 9 hierzu erforderlich wäre. Eine Bestimmung mittels numerischer Strömungsberechnungen ist derzeit noch nicht Stand der Technik.
Der Koeffizient wird daher über eine Schubmessung indirekt bestimmt.

$$ C_{v9} = \frac{w_{9,real}}{w_{9,ideal}} = \frac{ \left( \frac{F_9}{\dot{m}_9} \right)_{real} }{ \left( \frac{F_9}{\dot{m}_9} \right)_{ideal} } = \frac{ \left( \frac{F_9}{\dot{m}_9 \sqrt{R_9 T_{t9}}} \right)_{real} }{ \left( \frac{F_9}{\dot{m}_9 \sqrt{R_9 T_{t9}}} \right)_{ideal} } $$

$$...$$

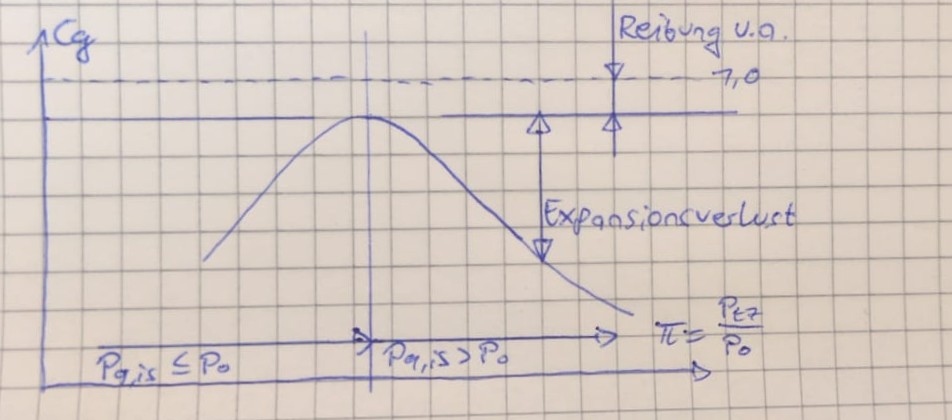
Der Bruttoschubkoeffizient

$$C_g = \frac{F_{9,real}}{F_{9,ideal}} \leq 1$$

Der Bruttoschubkoeffizient erfordert, ähnlich wie der Geschwindigkeitskoeffizient eine präzise Messung der Düsenkräfte und der anderen zu messenden Parameter. Eine Bestimmung mittels numerischer Strömungsberechnung ist derzeit noch nicht Stand der Technik.

$$ C_{g} = \frac{F_{9,real}}{F_{9,ideal}} = \frac{ \left( \frac{F_9}{A_8 \cdot p_0} \right)_{real} }{ \left( \frac{F_9}{A_8 \cdot p_0} \right)_{ideal} } $$

$$...$$

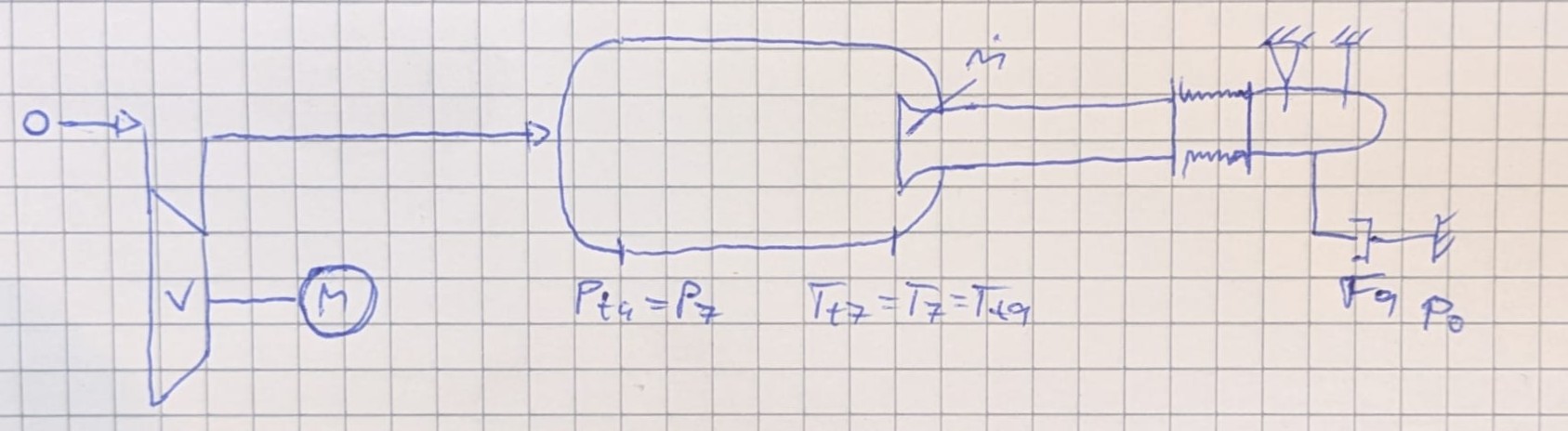
Ähnlichkeit bei durchströmten Komponenten - mit Wärmezufuhr

Physikalisch - chemischen Komponente in der Brennkammer

• Kraftstoff einbringen, zerstäuben
• Kraftstoff verdampfen
• Mischung mit Luft und Heißgas
• Reaktion
• Nachreaktion
• Zumischung zum Erreichen einer geeigneten Temperaturverteilung

Zu komplex zu berechnen - Vereinfachung mit reaktionsdominiertem Verbrennungsvorgang

Es wird angenommen, dass der Verbrennungsvorgang durch die Reaktion dominiert ist. Diese Reaktionsgrad – Theorie ist begründet auf den Untersuchungen von Arrhenius 1889.

Ähnlichkeiten bei Turbomaschinen - Verdichter

Die Ableitung von Ähnlichkeitsparametern kann auf zwei Arten erfolgen:

• Dimensionsanalyse
• Plausibilität

Im Rahmen der Vorlesung Turboflugtriebwerke wird dazu ein gedankliches Experiment mit durchgeführt. Es wird angenommen, dass ein einstufiger Axialverdichter auf einem Prüfstand erprobt wird.

• Über die Drossel D1 wird der Druck in der Beruhigungskammer eingestellt.
• Mit dem Wärmetauscher WT wird die Temperatur in der Beruhigungskammer eingestellt.
• In der Beruhigungskammer P herrschen sehr geringe Geschwindigkeiten, so dass totale und statische Größen annähernd gleich sind.
• Der Axialverdichter wird mit einem Motor M bei konstanter Drehzahl N gehalten.
• Über die Drossel D2 wird der Verdichter angedrosselt.

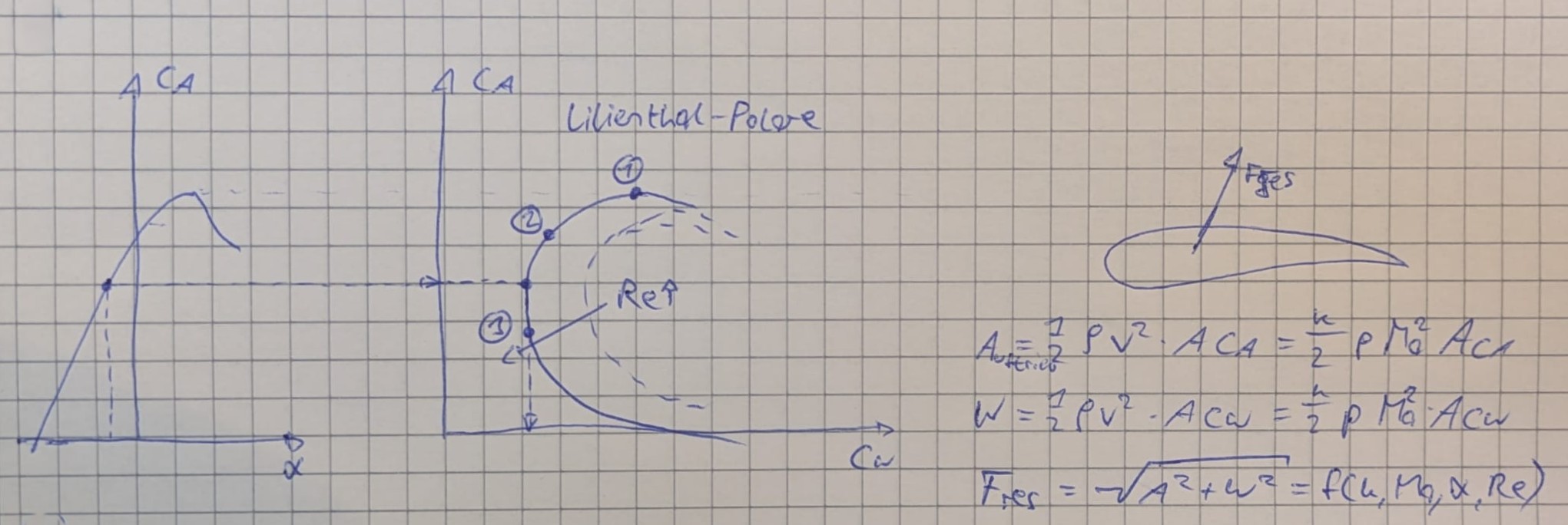
Ergänzung auf Folie 59: direkt nach dem Kessel (P) wird der Massenstrom $\dot{m_2}$ gemessen
Übung erklärt, warum Drosseln im Aufbau nötig sind

These: Eine Turbomaschine arbeitet in einem ähnlichen Betriebspunkt, wenn die Rotor- und Statorschaufeln im gleichen Winkel und mit gleicher Machzahl angeströmt werden.

Dazu betrachten wir den Verdichter auf dem sogenannten „Euler – Radius“, d.h. auf einer ringförmigen Fläche auf der die Strömung für den gesamten Verdichter repräsentativ ist. Diese Betrachtung wird auch Mittelschnitts – Betrachtung genannt. Wir nehmen an, dass der Verdichter aus dem Plenum gleichförmig und drallfrei angeströmt wird. Damit ergeben sich die nachfolgend abgebildeten Geschwindigkeitsdreiecke

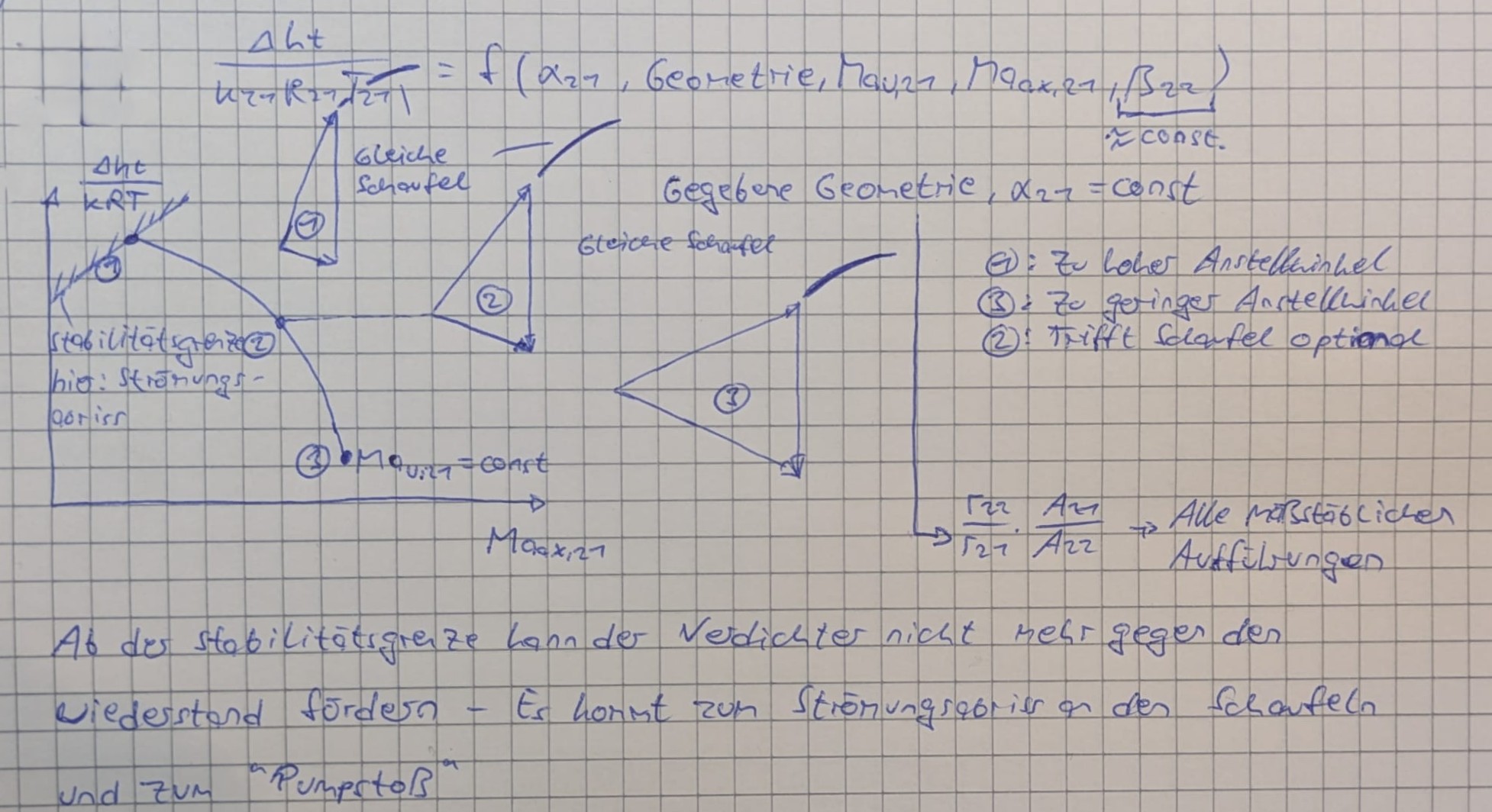
Rote Blöcke auf Folie 62 zeigen die wichtigsten Rechnungen, die man sich merken sollte

Sowohl bei drallfreier Anströmung als auch bei drallbehafteter Anströmung sind Anströmwinkel und Anströmmachzahl des Rotors konstant sind, wenn die Umfangs- machzahl und die axiale Machzahl konstant sind.

Die Parameter des Kennfelds enthalten

• die Ringraumfläche A21
• den Eulerdurchmesser DE21
• die individuelle Gaskonstante (abhängig von der molaren Masse des Gases)
• den Isentropenexponenten (Zustandsfunktion, abhängig von der Gaszusammensetzung)
• den statischen Druck und die statische Temperatur am Rotoreintritt.