Turboflugtriebwerke - Düsen

14 April 2025, Stephan Staudacher

Ähnlichkeiten bei durchströmten Komponenten

$$\frac{m_2 \sqrt{RT_{t2}}}{A_2 P_{t2}} = f(x, Ma_2), [-] = \frac{\dot{m_2} \sqrt{RT_{t2}}}{P_{t2}, [m^2]}$$

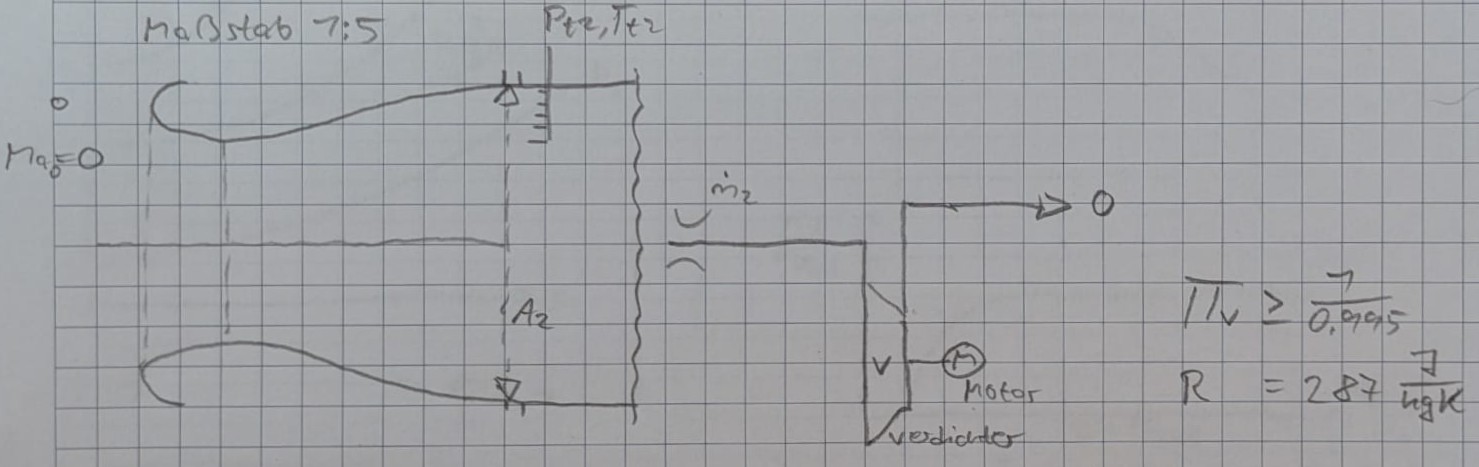
Aus der Messung:
$p_{t0} = p_0$
$p_{t2/t0} = p_0$
$\frac{\dot{m_2} \sqrt{RT_{t2}}}{P_{t2}, [m^2]}$\

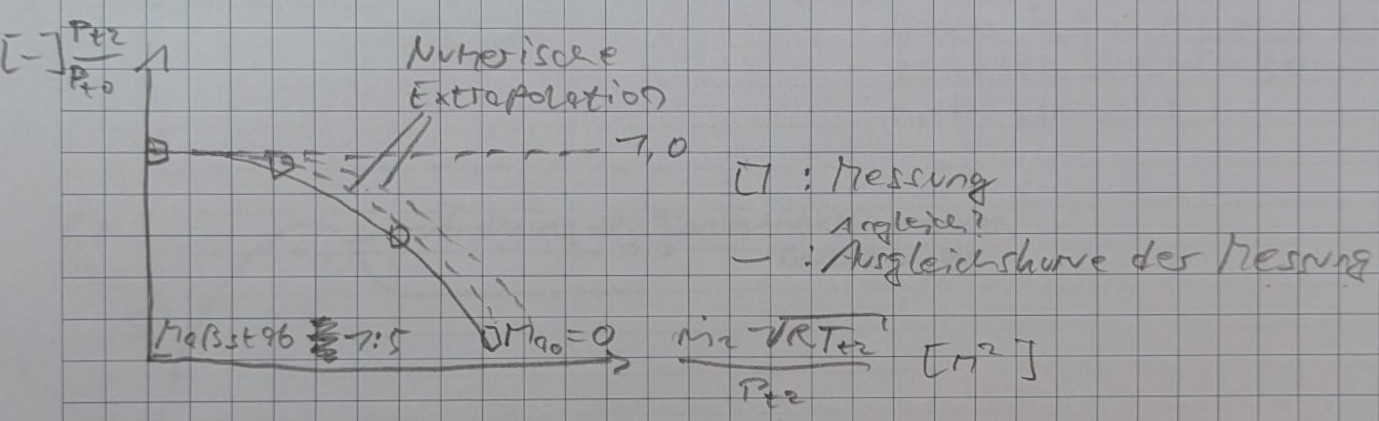
Problem, das Original mithilfe des Kennfelds mit Maßstab 1:5 betreiben zu dürfen, weil das Kennfeld noch dimensionsbehaftet ist $[m^2]$
Daher: Übertragung auf Kennfeld ohne Dimension

$$\downarrow$$

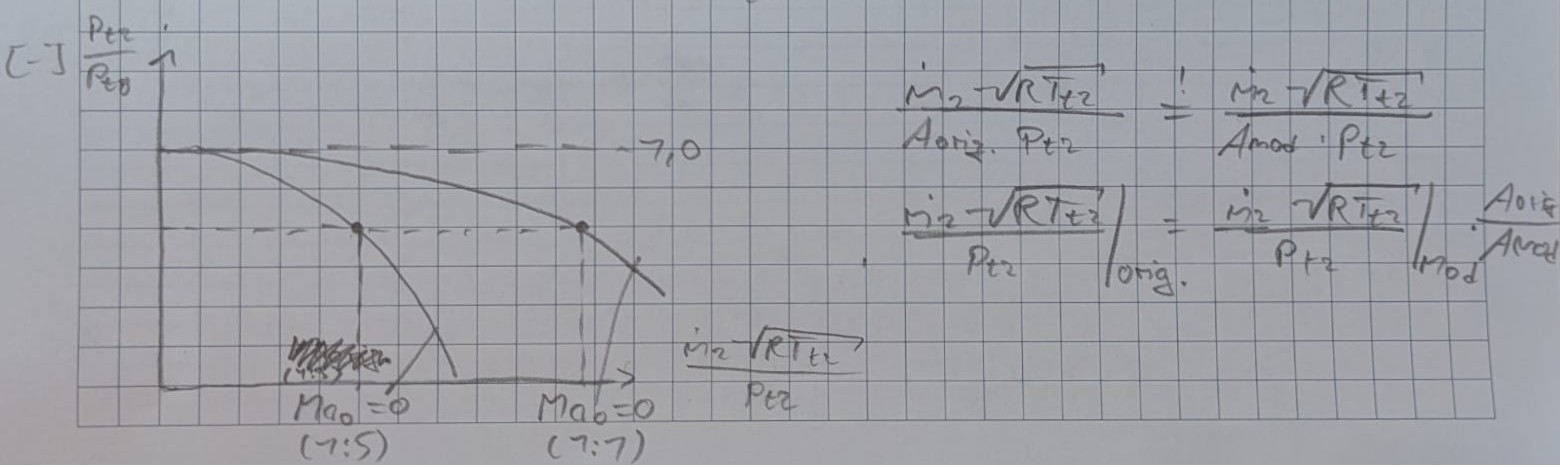
Ähnlichkeiten bei durchströmten Komponenten - Strömungskanäle

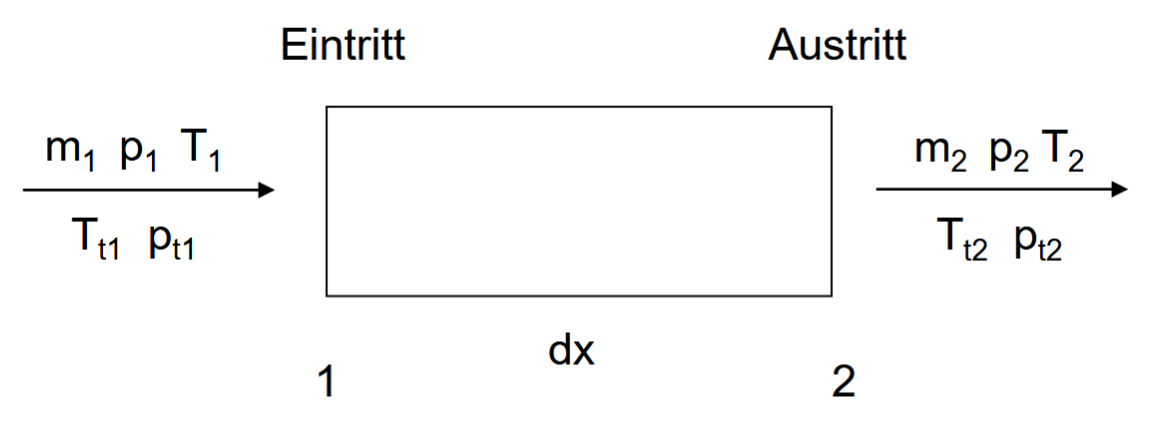
Es wird angenommen, dass in den Strömungskanälen technische Arbeit weder zu- noch abgeführt wird. Darüber hinaus wird angenommen, dass keine Wärme zu- oder abgeführt wird, es gilt somit: $T_{t1} = T_{t2}$
Wandreibungsspannung wird unter Annahme einer vollausgebildeten Strömung mit Hilfe des Rohreibungskoeffizienten $\lambda$ beschrieben:

$$\tau_w = \frac{\lambda}{8} \rho w_1^2$$

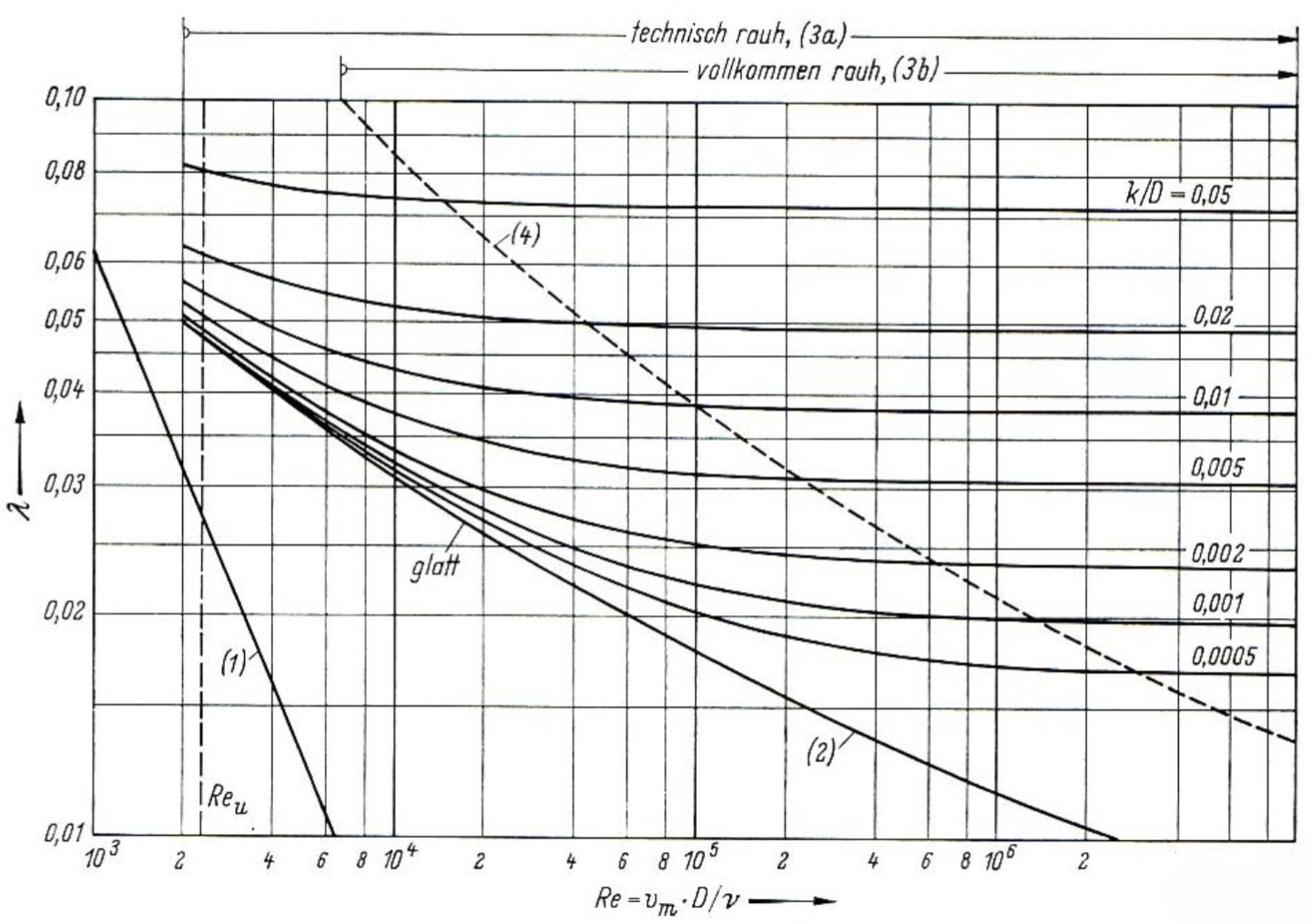
Zahlenwert für $\lambda$ kann aus Moody-Diagramm abgelesen werden.

Ähnlichkeiten bei durchströmten Komponenten - Düsen

Düsensysteme werden unterschieden nach

• dem Querschnittsverlauf
  • konvergent
  • konvergenz-divergent
• der verstellbarkeit
  • feste geometrie
  • variable geometrie

Heute verwendete Triebwerke (Zivil, Unterschall) sind Zweistrom-Turboluftstrahl-Triebwerke mit fester Geometrie. Unterschied:

• Düsen für jeden Strom (seperate jets)
• Düse für beide Ströme (mixed flow)

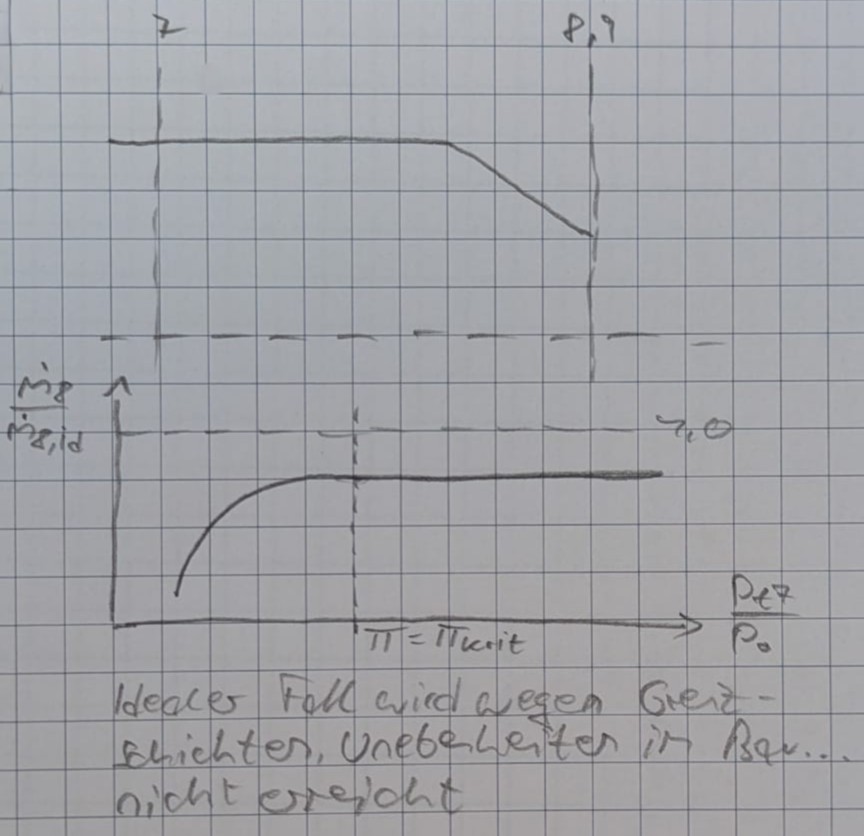
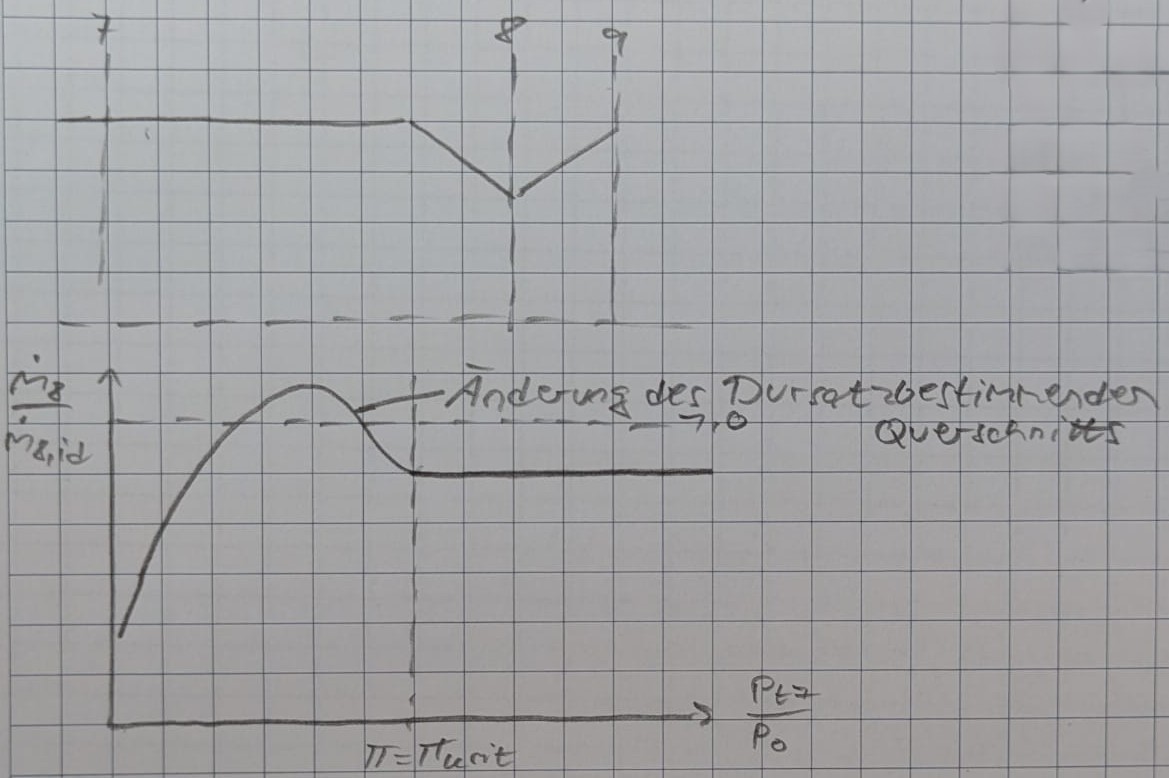
Warum bricht die Kurve vor $\Pi_krit$ ab? Wegen einem Reynoldszahl-Effekt der konvergenten Düse
Bei einer Konvergent-Divergenten Düse sieht der Verlauf anders aus: