System Design 1 - Vorlesung

16 April 2025, Bastian Luettig

State transfer functions

Signal transfer function $T$: Changes the input signals to output signals depending on the mode $s_{mode}$
State transfer function $Z$: Changes the input states and platform states $\underline{z}_{pf}$ to output states
Evaluation function $\varepsilon$: Returns the maximum available degradation a system can perform - based on the input states

• We can describe the overall system behavior using the transfer function $T$
• Alongside the normal signal transfer functions $T$, we can use state transfer functions $Z$ to describe state changes
• We can compise and decompose state transfer function
• We can input fectors into signal and state transfer function
• Evaluation functions reduce vectors to scalars

transfer functions for the redundant system

• sfu - system function (?)
• rf - redundant flight control computer
• ra - redundant actuator
• rs - redundant sensor
• nl - normal law
• al - alternate law
• dl - direct law
• p - passive
• o - out of control

(Can be written as text in exam, but has to be precise)

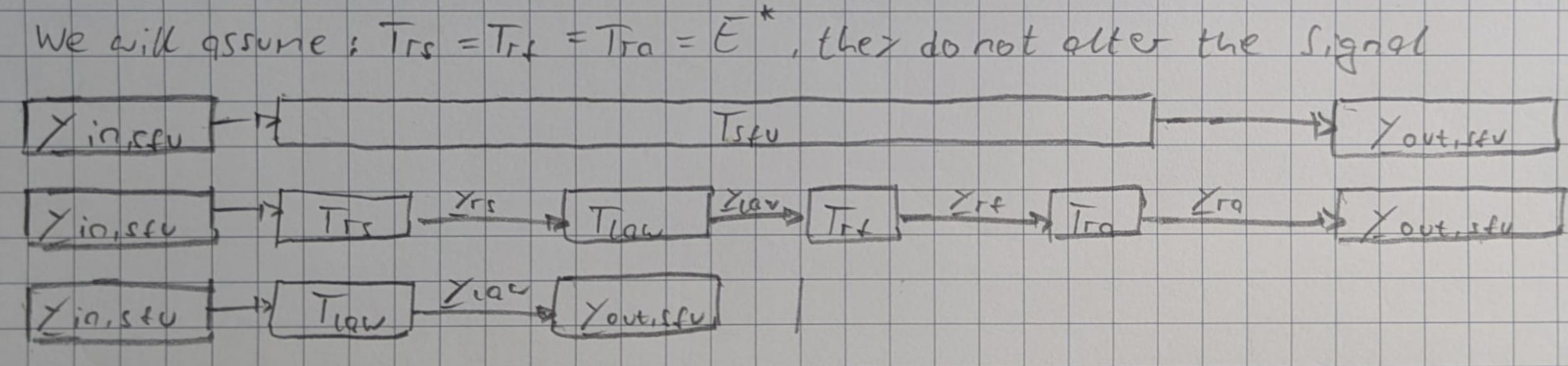
With the simplification above, the overall signal transfer function becomes:

$$T_{sfu} = T_{ra} \circ T_{rf} \circ T_{law}(s_{mode}) \circ T_{rs}(\underline{y}_{in, sfu})$$

$$T_{sfu} = T_{law}(s_{mode}, \underline{y}_{in, sfu})$$

How do we find $Z_{law}$?

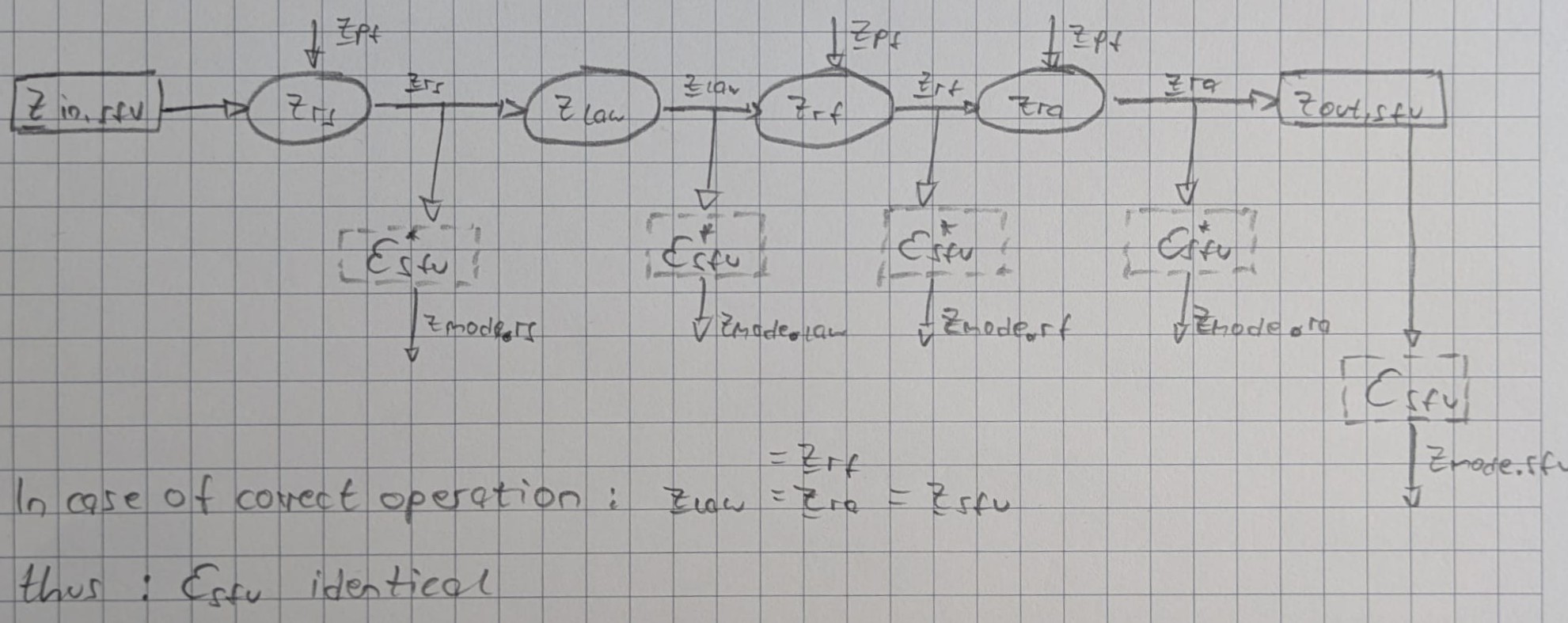
The following can usually be easily obtained:

• $E^*_{sfu}$
• $Z^*_{law}$

(Slide 24 diagram will be given in exam, but we need to know how to work with it)

Signals:

$$\underline{y}{sfu} = T{law}(s_{mode.law},\underline{y}_{in-sft})$$

States: (correct order of the function is important)

$$\underline{z}{sfu} = {z}{sfu}(\underline{z}{pf}, \underline{z}{in.sft})$$

$$\underline{z}{sfu} = {z}{ra}(\underline{z}{pf}) \circ {z}{rf}(\underline{z}{pf}) \circ {z}^*{law}(z_{mode.law}) \circ {z}{rs}(\underline{z}{pf}, \underline{z}_{in.sfu})$$

Evaluation:

$$\varepsilon^*{sfu} = \varepsilon{sfu} \circ z_{law}$$

These functions can be used to decribe the whole system

• which inputs lead to which outputs
• system failures
• when does my system degrade to a specific mode?

How to use this information

$P(lossOfNormalLaw) = 10^{-4}$
$P(lossOfNormalLaw, alternateLaw) = 10^{-7}$
$P(lossOfNormalLaw, alternateLaw, directLaw) = 10^{-9}$

Using transfer functions, these laws can be expressed formally (see slide 27)

Creating the system requirements document YRD

To create the YRD, we need to:

• systematically find requirements for the system function
• formally define the requirements

To achieve this, we follow this process:

• develop the architecture
• develop degredation modes
• develop signals for each degredation mode
• develop functional requirements
• develop platform-dependent state transfer, evaluation functions
• allocate safety requirements

The resulting requirements form the YRD

basic arcitecture: what does the system do comprises of what each component does ($T_{sfu}$)\

Platform architecture (longest chapter in this course)

Generic state transfer functions for modules

Module A module refers ro any single or redundant hardware unit examples: signle sensor number 1 or type stick, redundant computer, single actuator elevator left hand

each module performs a state transfer function

• 1. each module has a state $z_{mod}$
• 2. the output states depend on:
  • the input states $\underline{z}_{in}$
  • the module's state $z_{mod}$
• 3. the output state is correct if:
  • the input states are correct
  • the modules state is correct

passivating a lane can be complicated, in this lecture, we simplify these cases by considering passive lanes to have no effect on the rest of the system