Strukturdynamik - Kapitel 10
27 June 2025, Malte Krack
Finite Elemente Methode - Diskretisierung
- Unterteilung in $N_e$ Elemente und $N_n$ Knoten (Vernetzen)
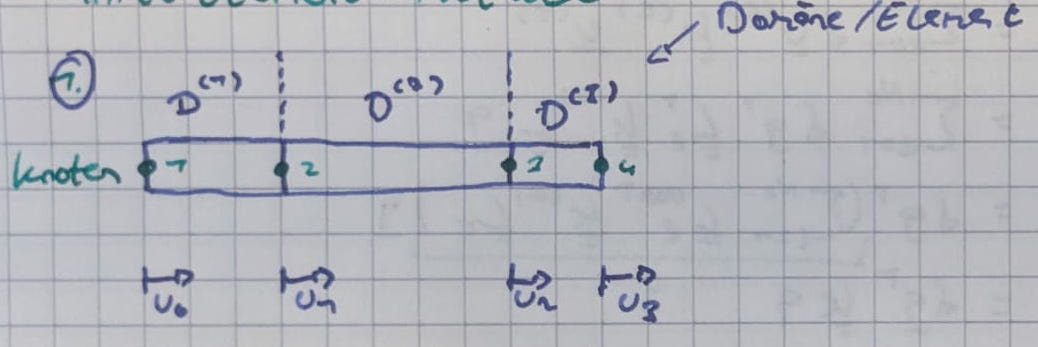
- Bestimmung der Koeffizientenmatrizen für jedes Element: $\underline{\underline{m}}^(e), \underline{\underline{k}}^(e), \underline{f}^(e)$ für jedes Element '$e$' isoliert. Festlegen der Ansatzfunktionen je Element (Elementtyp Wählen)
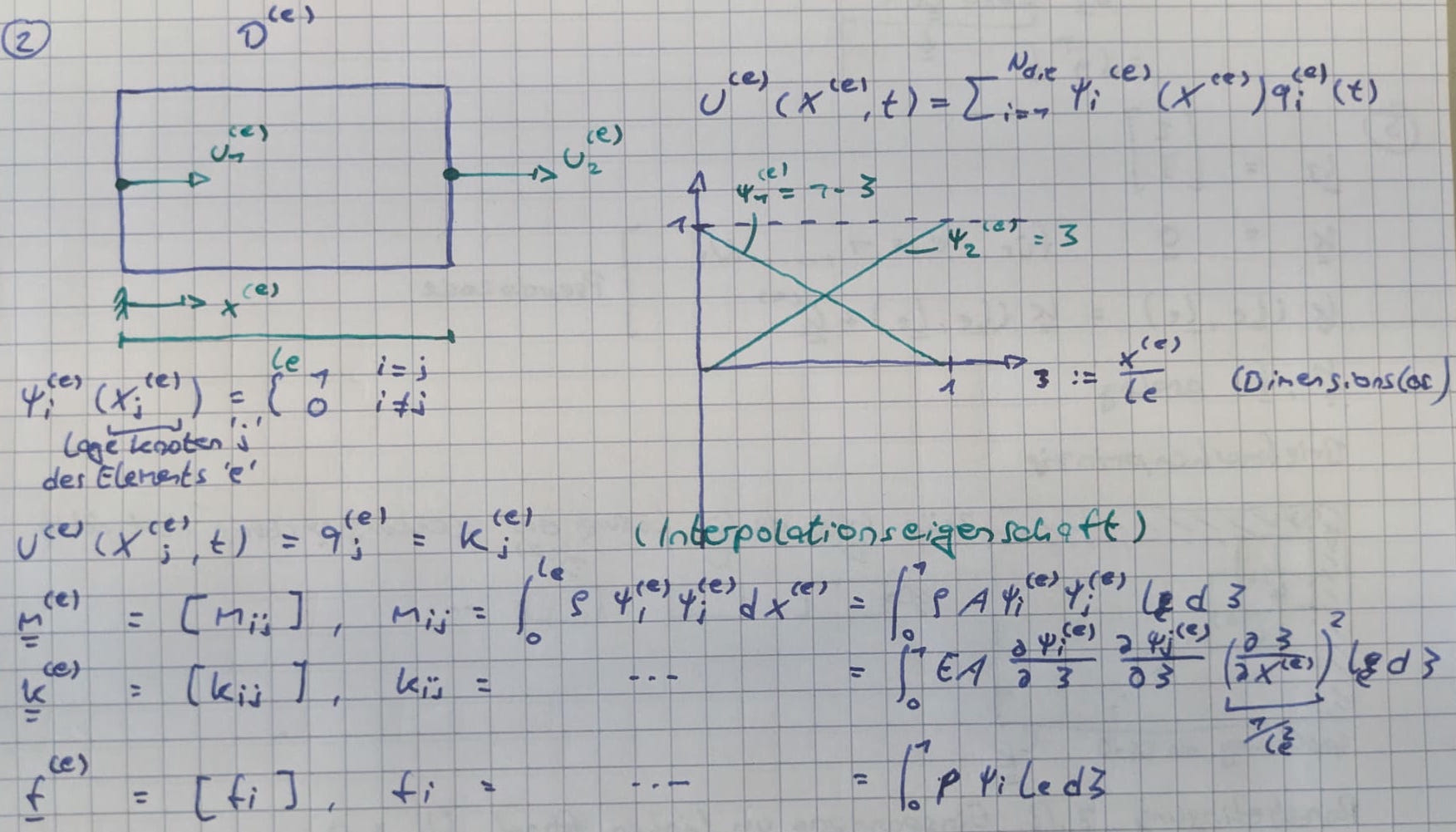
$$\underline{\underline{M}} = \sum_e \underline{\underline{L}}_e^T \underline{\underline{m}}^{(e)} \underline{\underline{L}}_e$$
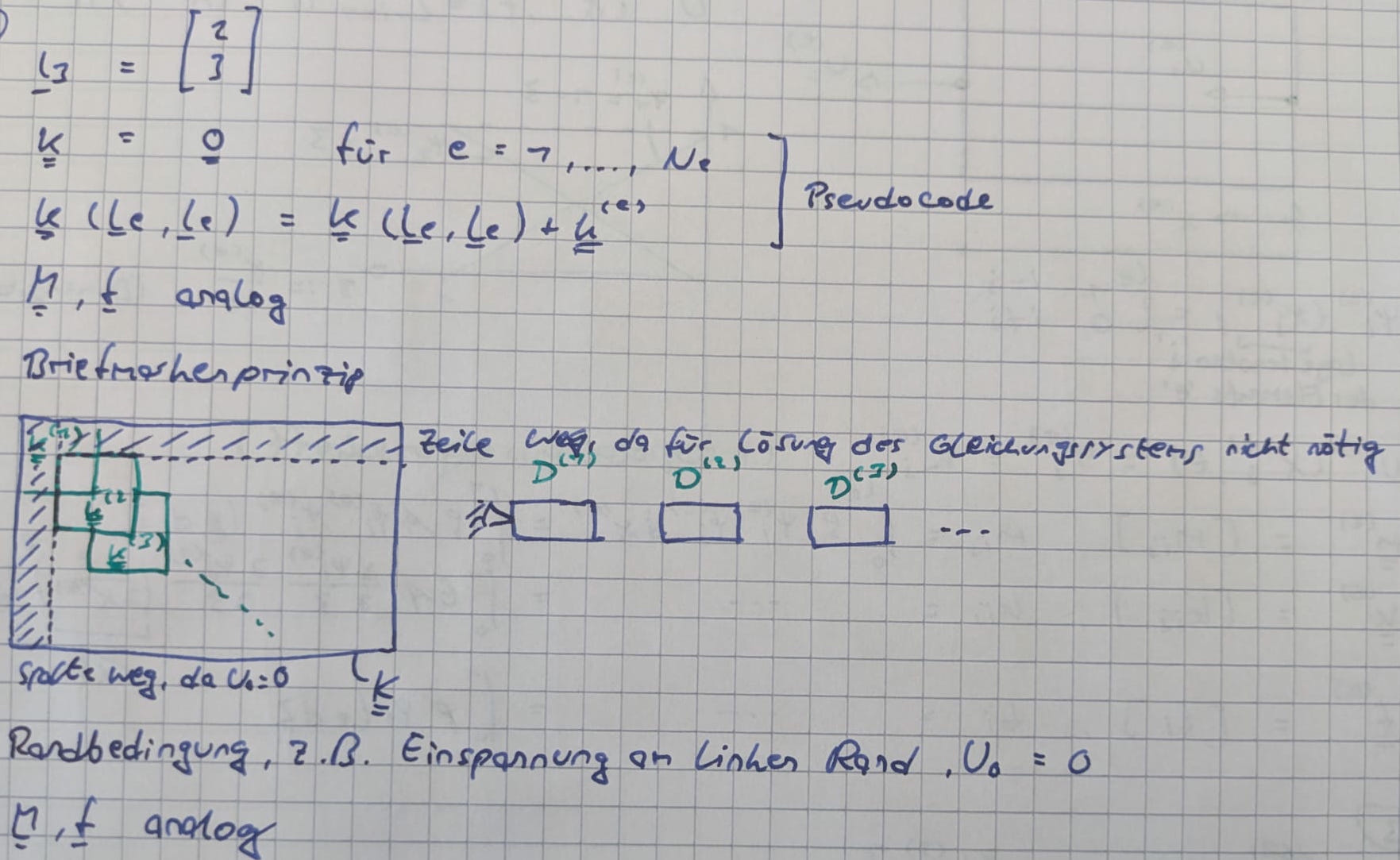
- Zusammenbau des Gleichungssystems (Assembly)
Kinematische Verträglichkeit: Dank Interpolationseigenschaft einfach gemeinsame Knoten-FHG an Elementrändern fordern $\hat{=}$ Globalen Ansatz stetig machen (Vereinigung der lokalen Ansätze)
Beispiel:

Herleitung über virtuelle Arbeit

Ökonomischere Berechnung:
$$\underline{\underline{L}}_e \rightarrow \underline{l}_e$$
Eigenschaften von $\underline{\underline{M}}, \underline{\underline{K}}$:
- Dünn besetzt
- Bandstruktur (bei geeigneter Sortierung)