Strukturdynamik - Kapitel 5

13 May 2025, Malte Krack

Eigendynamik konservativer Mehr-Freiheitsgrad-Systeme

Ruhelage indiferent

$$\rightarrow \underline{\underline{K}} \lt 0$$

Es gibt $\underline{\varphi_j} \neq \underline{0}$ sodass $\underline{\underline{K}} \underline{\varphi_j} = \underline{0}$

$$\rightarrow \tilde{\underline{q}}(\underline{t}) = \underline{\varphi_j} \eta_j(t) \rightarrow \underline{\underline{M}}\underline{\varphi_j} \ddot{eta}_j + \underline{\underline{K}} \underline{\varphi_j} \eta_j = \underline{0}$$

$$\ddot{\eta}_j = 0, \eta_j(t) = \alpha_j + \beta_j \cdot t$$

$$\omega_j^2 = \tilde{\lambda}_j = - \frac{\ddot{\eta}_j}{\eta_j} = 0$$

$\rightarrow \quad \underline{\varphi}_j$ sind Eigenvektoren zu $\tilde{\lambda}_j = 0$
$\rightarrow$ Da sie keine elastische Kraft bewirken ($\underline{\underline{K}} \cdot \underline{\varphi}_j$) nennt man sie Starrkörpermoden, die übrigen elastische Moden

Ruhelage instabil

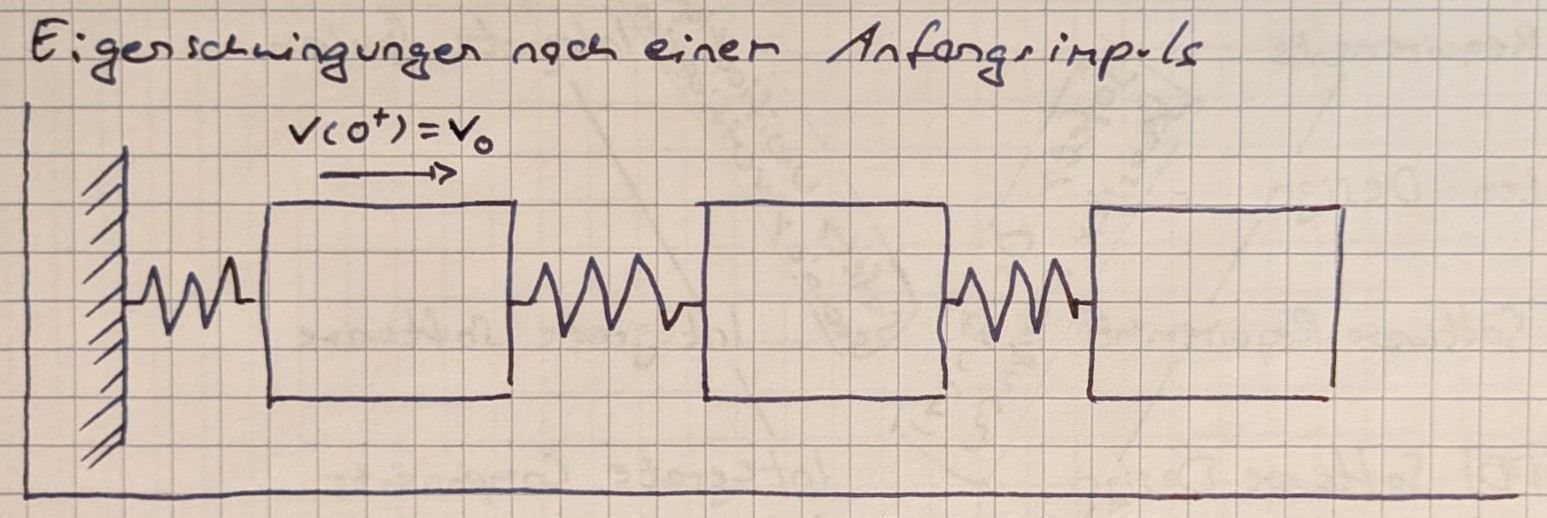
Zurück: Wie lässt sich die – auf den ersten Blick regellose – Schwingung nach einem Anfangsimpuls deuten?

• Sie setzt sich aus n Anteilen (zeitlich) harmonischer Oszillationen zusammen
• Frequenz und räumliche Form dieser Anteile erhält man als Lösung eines verallgemeinerten Eigenwertproblems.
• Bei Systemen mit indifferenter Gleichgewichtslage entarten die Teilschwingungen mit Eigenfrequenz Null zu gleichförmigen Bewegungen