Strukturdynamik - Kapitel 4
06 May 2025, Malte Krack
Wiederholung: Vorgehen nach Newton-Euler
- Freischneiden der Einzelkörper, Eintragen der Reaktionskräfte und -momente
- Aufstellen von Impuls- und Drallsätzen je einzelnem Körper $i$.
Für ebene Bewegungen starrer Körper (x-y-Ebene):\
Impulssätze:
$$m_i \ddot{x} c_{,i} = \sum_j F_{j,x}$$
$$m_i \ddot{y} c_{,i} = \sum_j F_{j,y}$$
Drallsatz:
$$J_i^{(A)} \ddot{\varphi} _i = \sum_k M_{k}^{(A)}$$
- Wahl verallgemeinerter Koordinaten, Eleminieren der Reaktionskräfte/ -momente und übrigen Koordinaten (unter Ausnutzung kinematischer Zwangsbedingungen)
Drallsatz gilt in dieser einfachern Form nur, falls Punkt A Schwerpunkt oder raumfester Punkt des Körpers ist
Wiederholung: Vorgehen nach Lagrange
- Bestimmen der kinetischen und potentiellen Energie des Gesamtsystems
kinetische Energie eines sich in der x-y-Ebene bewegenden Starrkörpers $i$:
$$E_k^i = \frac{1}{2} m_i (\dot{x}^2 _{C,i} + \dot{y}^2 _{C,i}) + \frac{1}{2} J_{zz,i}^{(C)} \dot{\varphi} _{z,i}^{2} = \frac{1}{2} J_{zz,i}^{(Q)} \dot{\varphi} _{z,i}^{2}$$
$$Q: \text{raumfester Punkt (allgemein: Momentanpol)}, C: \text{Schwerpunkt}$$
Potenzielle Energie (Beispiele):
$$E_p = \frac{1}{2} k \Delta l^2$$
$$E_p = m g h$$
- Wahl der verallgemeinerten Koordinaten $q_s, \quad s=1,2,\dots, n$
- Bestimmen der verallgemeinerten Kräfte infolge incht-konservativer Kräfte und Momente (ebener Fall)
$$Q_s^{nk} = \sum_i F_{i,x}^{nk} \frac{\partial \dot{x} _i}{\partial \dot{q} _s} + F_{i,y}^{nk} \frac{\partial \dot{y} _i}{\partial \dot{q} _s} + \sum_j M_{j,z}^{nk} \frac{\partial \dot{\varphi} _{j,z}}{\partial \dot{q} _s}$$
- Aufstellen der Lagrange'schen Gleichungen
$$\frac{d}{dt}(\frac{\partial E_k}{\partial \dot{q}_s}) - \frac{\partial E_k}{\partial q_s} + \frac{\partial E_p}{\partial q_s} = Q_s^{nk}, \quad s=1,2,...,n$$
System an allgemeinen Bewegungsdifferentialgleichungen eines Mehrkörbersystems
$$\underline{r}(q, \dot{q}, \ddot{q}, t) = \underline{0}, ...$$
$\rightarrow$ gewöhnliches DGL-System
$\rightarrow$ nichtlinear in $q, \dot{q}$\
Linearisierung
Interessant, wenn ein kleiner Bereich um eine gegebene Situation gesucht ist
$\rightarrow$ Oft relevant: kleine Bewegungen um ein gegebenes $q^*(t)$
$$q = q^*(t) + \Delta q$$
Entwicklung mithilfe ver Taylor-Entwicklung von $\underline{r}$ um $q^*(t)$

Ruhelage (im statischen Sinne) stabil, wenn $E_p$ minimal

Aufspalten nach Symmetrien
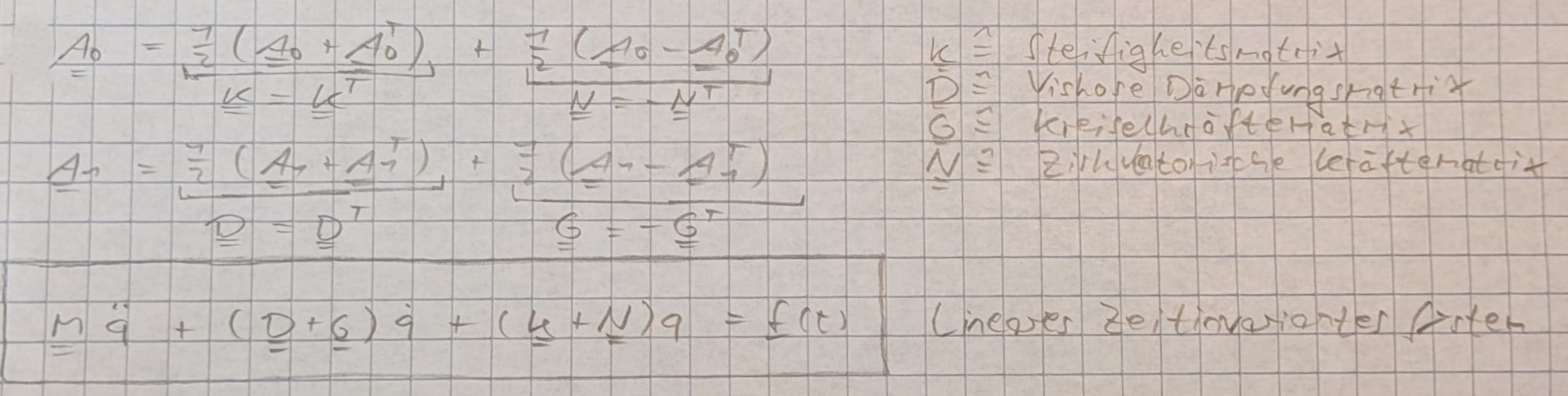
Leistungsbilanz und Berechnungsbeispiel (Bewegungsgleichung von Schwingungsketten) im Vorlesungsaufschrieb 4 auf Ilias