Strukturdynamik - Vorlesung

15 April 2025, Malte Krack

Erzwungene Schwingungen von Ein-Freiheitsgrad-Systemen

Beispiel Flugzeug rollt über eine unebene Fahrbahn

• Wie stark federt das Flugzeug ein?
• Sind alle Bodenwellen gleichermaßen schädlich?

Unebenheiten dargestellt durch Bewegungen des Feder-Dämpfer-Fußpunktes
Annahmen: Bugrad hebt nie ab, Rad klein gegenüber Bodenwellen
Wir behandeln zunächst eine rein harmonische Anregung, später verallgemeinern wir auf periodische und beliebige Anregungen

$$q = x-x_0, \dot{q} = \dot{x}, \ddot{q} = \ddot{x}$$

$$\rightarrow m \ddot{q} = - m g - k (x_0 + q - u - l_0) - d(\dot{q} - \dot{u}) $$

Alle unbekannten Terme auf die linke Seite und kürzen ergibt zusammengefasst:

$$\rightarrow m\ddot{q} + d \dot{q} + k q = k u(t) + d \dot{u}(t) \quad \quad Gleichung Nummer 1$$

Linear, mit konstanten Koeffizienten, gewöhnliche DGL, zweiter Ordnung, im Gegensatz zum letzten mal hier eine inhomogene DGL
Statische Kräfte wie die Gewichtskraft treten hier, aus der Ruhelage heraus, nicht mehr auf
Zum lösen die Anregung $u(t)$ genauer beschreiben:

Nützliche Folie 59 und 60 über Darstellung harmonischer Funktionen und komplexen Ergänzungen

Exponentialdarstellung:

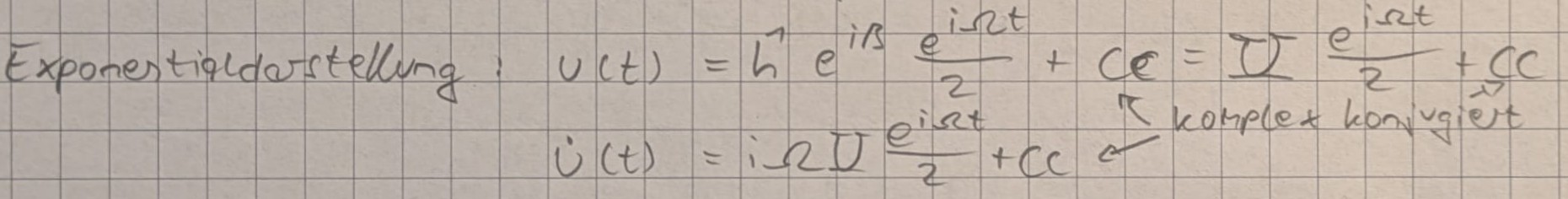
Partikuläre lösung wird heute behandelt
Ansatz vom Typ her eine homogene Lösung:

$$q_p(t) = Q \frac{e^{i \Omega t}}{2} + cc; \quad \quad Q, U \in \mathbb{C} $$ $$\dot{q}_p(t) = q \Omega Q \frac{e^{i \Omega t}}{2} + cc$$ $$\ddot{q}_p(t) = -\Omega^2 Q \frac{e^{i \Omega t}}{2} + cc$$

Für kleine Frequenzen ($\Omega$) dominiert der statische Anteil, für große Frequenzen dominiert die Masse und damit die Trägheitskräfte im System
Beweis im Vortragsmitschrieb

$$...$$

Bei welcher Frequenz tritt die maximale Vergrößerung (Schwingungsantwort auf?)

Notwendige Bedingung: Ableitung der Vergrößerungsfunktion nach dem Frequenzverhältnis muss verschwinden

$$\frac{dV}{dr} = \frac{d}{dr}(\frac{\sqrt{1+(2Dr)^2}}{\sqrt{(1-r^2)^2+(2Dr)^2}}) = 0$$

$$R = 0 \quad oder \quad 2D^2r^4+r^2-1 = 0$$

$$r_{max} = \sqrt{\frac{\sqrt{1+8 D^2}-1}{4D^2}}$$

Für $0 <= D << 1 \quad \quad r_{max} = 1$

Amplituden- und Phasenfrequenzgang hänge con der Art der Anregung ab
Resonanzerscheinungen treten für leichte Dämpfungen aber stets für Anregungsfrequenzen nahe der Eigenfrequenz auf

Modellgleichung:

$$\ddot{q} + 2 D \omega \dot{q} + \omega^2 q = \omega^2 u(t) + 2 D \omega \dot{u}(t)$$

Harmonische Anregung:

$$u(t) = \mathfrak{R} [ U e^{i \Omega t} ] $$

Allgemeine Lösung:

$$q(t) = \mathfrak{R} [|Q| e^{i(\Psi_u+\Delta\Psi)}e^{i\Omega t}]+q_h(t)$$

Periodische Anregung

Froße Amplituden, wenn die Anregungsfrequenz einem Vielfachen der Eigenfrequenz entspricht, jedoch nimmt die Schwingungsantwort Amplitude mit abnehmender Anregungsfrequenz ebenfalls ab

Mitellage: Peak-to-Peak Hälfte

Bei periodischen Anregungen treten Resonanzen nicht nur auf, wenn die Grundfrequenz $\Omega$ der Anregung die Eigenfrequenz $\omega$ trifft, sondern auch wenn Vielfache der Grundfrequenz $n \Omega$ die Eigenfrequenz treffen.

Nicht alle Anregungen sind periodisch

In deterministischen Systemen erhält man unter denselben Bedingungen dasselbe Ergebnis
Bei nicht-deteministischen Systemen ist dagegen eine "zufällige" Streuung überlagert (Nicht Bestandteil der Lehrveranstaltung)

Harmonische und periodische Anregungen sind typisch für Maschinen mit rotierenden Komponenten

Transiente Anregung ist im grunde periodisch, aber mit zeitveränderlichen Parametern