Strukturdynamik - Kapitel 2
11 April 2025, Malte Krack
Eigendynamik von Ein-Freiheitsgradsystemen
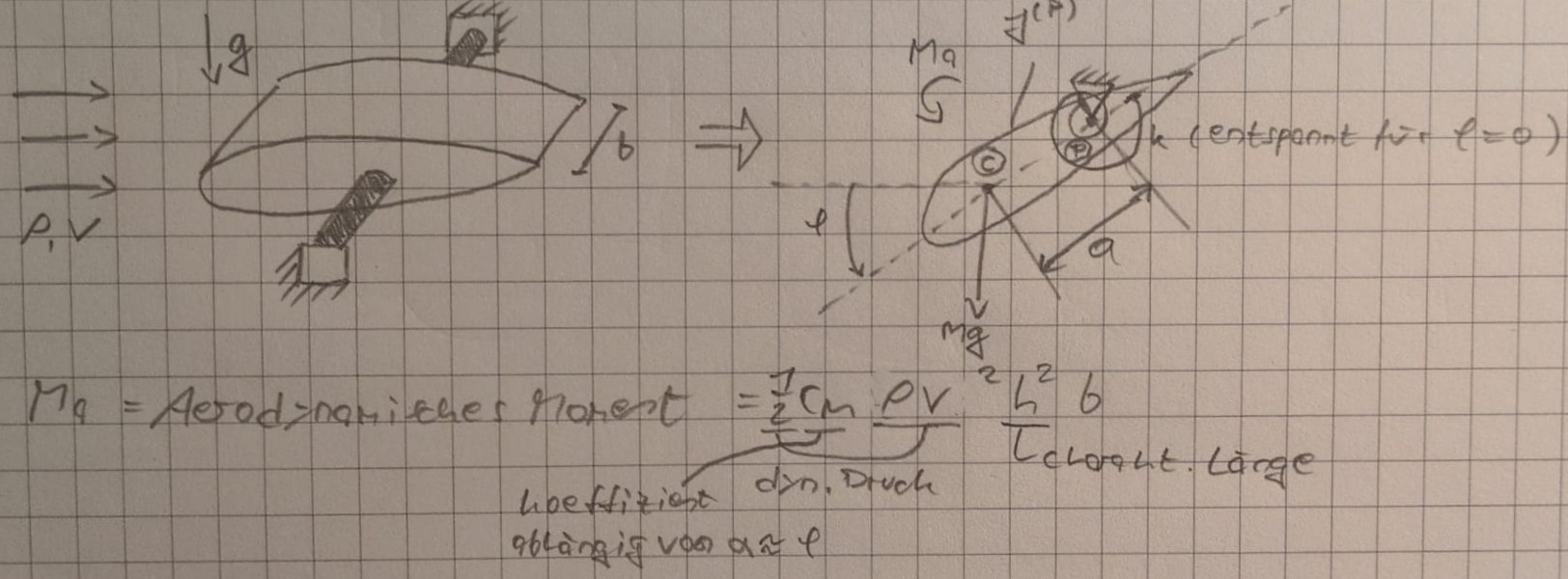
$$M_a = c_m \frac{\rho v^2}{2} h^2 b$$ Drallsatz für $p$ raumfest: $$J^{(p)} \ddot{\varphi} = \sum M^{(p)}$$ $$= M_a - k \varphi + m g a cos(\varphi)$$ $$J^{(p)} \ddot{\varphi} = -k\varphi + m g a cos(\varphi) + \frac{\delta^2}{2} h^2 b w' \varphi$$ $$...$$
Mit $J^{(p)}$ = Flächenträgheitsmoment um Punkt p Mit $M_R(\varphi)$ = Rückführendes Moment
Ruhelagen
Es gilt $\varphi = \varphi_0 = const \rightarrow \dot{\varphi} = 0 = \ddot{\varphi}$ $\rightarrow M_R(\varphi_0) != 0 \rightarrow k^* \varphi_0 = m g a cos(\varphi_0)$
Stabilität der Ruhelage $\varphi_0$
Kleine Auslenkungen $\Delta\varphi = \varphi - \varphi_0$ bleiben klein $\delta\varphi \rightarrow 0$
Ruhelage $\varphi_0$
stabil für: $\frac{M_R}{d\varphi}<0$, $E_p$ hat Minimum
instabil für $\frac{M_R}{d\varphi}>0$, $E_p$ hat Maximum
Für $\frac{M_R}{d\varphi}=0$: Keine Aussage nach linearer Theorie möglich
Potentielle Energie $E_p = - \int M_R d \phi$
Wie schwingt es?
Annahme: kleine Auslenkungen $\Delta\varphi = \varphi - \varphi_0$ um stabile Ruhelage $\varphi_0$
Taylor-Entwicklung: $M_R(\Delta\varphi) ~= M_R(\varphi_0) + \frac{dM_R}{d\varphi} * \Delta\varphi + \Phi(\Delta\varphi^2)$
$M_R(\varphi_0) = 0, \Phi(\Delta\varphi^2) = 0, \frac{dM_R}{d\varphi} = -k, k = 0$
Linearsierte Bewegungsgleichung
$$J^{(p)} \ddot{\varphi} = -k\Delta\varphi, \Delta\dot{\varphi} = \dot{\varphi}, \Delta\ddot{\varphi} = \ddot{\varphi}$$ $$\rightarrow J^{(p)} \Delta\ddot{\varphi} + k\Delta\varphi = 0$$ Entspricht einem Feder-Masse-System
Differentialgleichung gilt für alle Ein-Freiheitsgrad-Systeme (EFS) - Standardform für EFS, frei, ungedämpft: $$\ddot{q} + \omega^2 q = 0$$
Standardform EFS, frei, gedämpft
$$\ddot{q} + 2 D \omega \dot{q} + \omega^2 q = 0$$ $$D, \omega \epsilon \mathbb{R}$$
Ansatz:
$\tilde{q} = Q e^{\lambda t}, \dot{\tilde{q}} = \lambda Q e^{\lambda t}, \ddot{\tilde{q}} = \lambda^2 Q e^{\lambda t}$
$\rightarrow [\lambda^2 + 2 D \omega \lambda + \omega^2] Q e^{\lambda t} = 0$
nichttriviale Lösung: $[\lambda^2 + 2 D \omega \lambda + \omega^2] \overset{!}{=} 0$
$\lambda_{1,2} = -D \omega \pm \sqrt{(D \omega)^2- \omega^2} = (-D \pm \sqrt{D^2-1}) \omega$
Doppelte Würzen für $D^2=1 \rightarrow D = \pm 1, sonst \lambda_1 \neq \lambda_2$
allgemeine lösung:
$\tilde{q} = Q_1 e^{\lambda_1 t} + Q_2 e^{\lambda_2 t}$ für $D \neq \pm 1$
$\tilde{q} = Q_1 e^{-D \omega t} + Q_2 t e^{-D \omega t}$ für $D = \pm 1$
Der Dämpfungsgrad D ergibt sich auch der Ursache und der Stärke der Einwirkung auf die Schwingungen des betrachteten Systems
Wie bestimmt man die statischen Gleichgewichtslagen (Ruhelagen) eines EFS
- Extremstellen der potenziellen Energie bzw. Nullstellen der verallgemeinerten Rückführkraft Wie ist das Eigenverhalten für kleine Schwingungen um eine stabile Ruhelage?
- Harmonische Schwingungen mit der Eigenfrequenz
- Die Eigenfrequenz lässt sich aus der linearisierten Bewegungsgleichung ablesen (abhängig von Trägheuits und Steifigkeitseigenschaften)
- Positive viskose Dämpfung bewirkt exponentielles Abklingen