Strukturdynamik - Vorlesung

08 April 2025, Malte Krack

Lernziele

• Welche Bedeutung haben Vibrationen in der lrt?
• Wie beschreibe ich die Dynamik mechanischer Systeme?
• Wie schwingt es? Was kann alles passieren?
• Wie kann ich die Schwingungen berechnen?

Vibrationen verstehen

Einfachster Prototyp eines schwingungsfähigen Systems ist das Feder-Masse-System

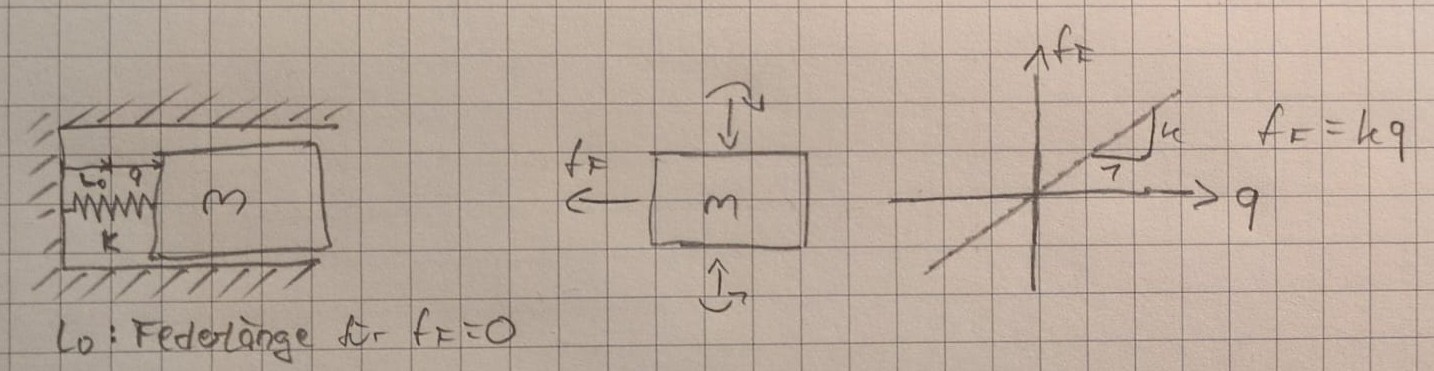
Impulssatz: Zeitliche Änderung des Impulses = Summer aller Kräfte in dieser Raumrichtung $$\frac{d}{dt}(mv)=sum(f)$$ $$m\ddot{q} = -f_F$$ DGL ist:

• gewöhnlich
• zweiter ordnung
• homogen
• linear mit konst. Koeffizienten

Allgemeine Lösung:

$$q = A cos(\omega t + \psi)$$ $$\dot{q} = -A \omega sin(\omega t + \psi)$$ $$\ddot{q} = -A \omega^2 cos(\omega t + \psi)$$

Allgemeine Lösung ist nicht die einzige mögliche Lösung, z.B. $A sin(\omega t + \psi)$ wäre auch möglich.

$$A = Amplitude, T = Periodendauer$$ $$\omega = Kreisfrequenz, \psi = Phasenlage$$ $$\omega T = 2 \pi$$ $$\omega = \frac{2 \pi}{T}$$

Einsetzen ergibt:

$$(-\omega^2 m + \kappa) A cos(\omega t + \psi) = 0$$

nichttriviale Lösung: $$\omega^2 = \frac{\kappa}{m}, \omega = \pm \sqrt{\frac{\kappa}{m}}$$

(Gilt nur für positive Koeffizienten)

Zeit eliminieren

Nutzen von $cos^2()+sin^2() = 1$

$$q^2 + \frac{\dot{q}}{\omega}^2 = A^2 cos(...)^2 + A^2 sin(...)^2 = A^2$$

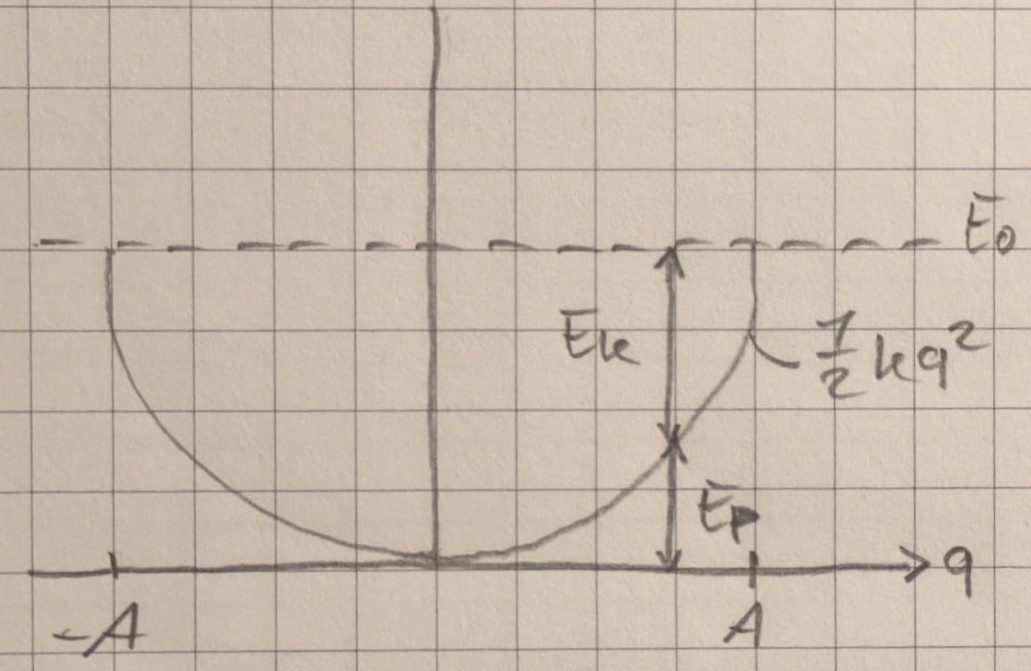
Kinetische Energie genau unter der Parabel, Potenzielle Energie genau darüber Bei $q=0$ ist potenzielle Energie maximal

• Einmaliger Anstoß, dann eigene Schwingung
• Selbsterregte Schwingungen
• Erzwungene Schwingungen durch äußere Störung
• Parametererregte Schwingung - Anregung des Systems durch von außen vorgegebene zeitliche Änderung von Parametern