Messverfahren des Wärmetransports - Lumped Capacitance Method

23 January 2026, Rico Poser

Anfangs isothermer Festkörper wird einem Temperatursprung unterzogen
Voraussetzung: zu jedem Zeitpunkt isothermer Körper

Energiebilanz

$$ h A [T_{aw} - T_w(t)] = m c_p \frac{\partial T_w}{\partial t} $$

$T_w(t)$ kann auch im inneren des Lumps gemessen werden, da dieser homogene Temperatur besitzt (angenommen)

$ \Psi_w(t) = T_{aw} - T_w(t) $

$ \rightarrow T_w(t) = T_{aw} - \Psi_w(t) $

$ \frac{d}{dt} T_w(t) = - \frac{d}{dt} \Psi_w(t) $

$ \frac{hA}{m c_p} \Psi_w(t) = -\frac{d}{dt}\Psi_w(t) $

$ \int_0^t -\frac{hA}{m c_p} d\tilde{t} = \int_{\Psi_i}^{\Psi} \frac{1}{\tilde{\Psi}} d\tilde{\Psi} $

$ -\frac{hA}{m c_p} t = ln(\frac{\Psi}{\Psi_i}) $

$ exp(-\frac{-h A}{m c_p} t) = \frac{T_{aw}-T_w(t)}{T_{aw}-T_i} $

$$ \frac{T_w(t) - T_i}{T_{aw} - T_i} = 1 - exp(-\frac{h A}{m c_p} t) $$

Ähnliche Form wie bei der unendlichen Wand Methode

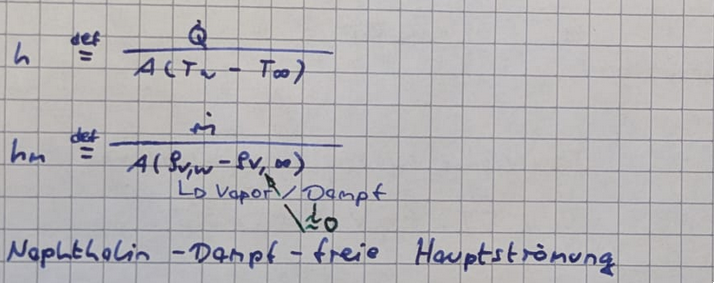
Analogien über den Massentransport

(Es geht um Massenaustausch zwischen Wand und Fluid) - Wie lässt sich dieser mit dem Wärmetransport zusammenbringen?

Diffusion - Wärmetransport

Testablauf

1. Bauteil mit Naphthalin beschichten
2. Anfangsoberflächenprofil oder Anfangsgewicht messen
3. Massentransport-Experiment durchführen (Strömung darüber leiten für die Sublimierung)
4. Endoberflächenprofil oder Endgewicht messen
5. Auswertung nach Massentransferkoeffizient $h_m$, Umrechnung in Sherwood-Zahl $Sh$
6. Übertragung auf die Nußelt-Zahl $Nu$ mittels Analogiefaktor $F$