Messverfahren des Wärmetransports - Konvektiver Wärmeübergang

31 October 2025, Rico Poser

Fouriersche Wärmeleitungsgleichung

Temperatur nicht mehr nur einzelne Größe, nicht mehr nur räumlich abhängig, sondern jetzt raum-zeitlich

Raum-zeitliches Temperaturfeld $T(\vec{x}, t)$

$$ \nabla \cdot k \cdot \nabla \cdot T + \dot{q} v = \rho c \frac{\partial T}{\partial t} $$

Vereinfachungen

Stationäre Probleme: $\frac{\partial T}{\partial t} = 0$

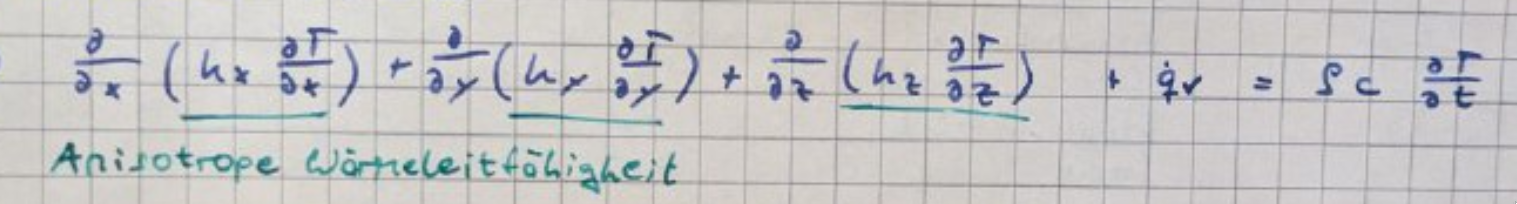
Wärmelitfähigkeit konstant und isotrop: $k = k_x = k_y = k_z = const.$

Stationäre Probleme bahezu unabhängig von Stoffeigenschaften, liegt an sehr langsamer Betrachtung bei stationären Problemen

Stationäres 1D Problem ohne Quellen und Senken: $\frac{d}{dx}(k \frac{dT}{dx}) = 0$

Wärmeübertragung durch Konvektion

Mechanismus ist mit Transport von Wärmeenergie-tragenden Teilchen verknüpft
Natürliche / freie Konvektion vs. erzwungene Konvektion

Exkurs: Grenzschichten

Konzentrationsgrenzschicht - gemeint ist die Stoffkonzentration, zum Beispiel Beschichtungen die durch Sublimation abgetragen werden
Strömungsgrenzschicht - liegt über den anderen Grenzschichten, heißt die anderen Schichten sind von dieser abhängig
Thermische Grenzschicht

Konzentrationsgrenzschicht

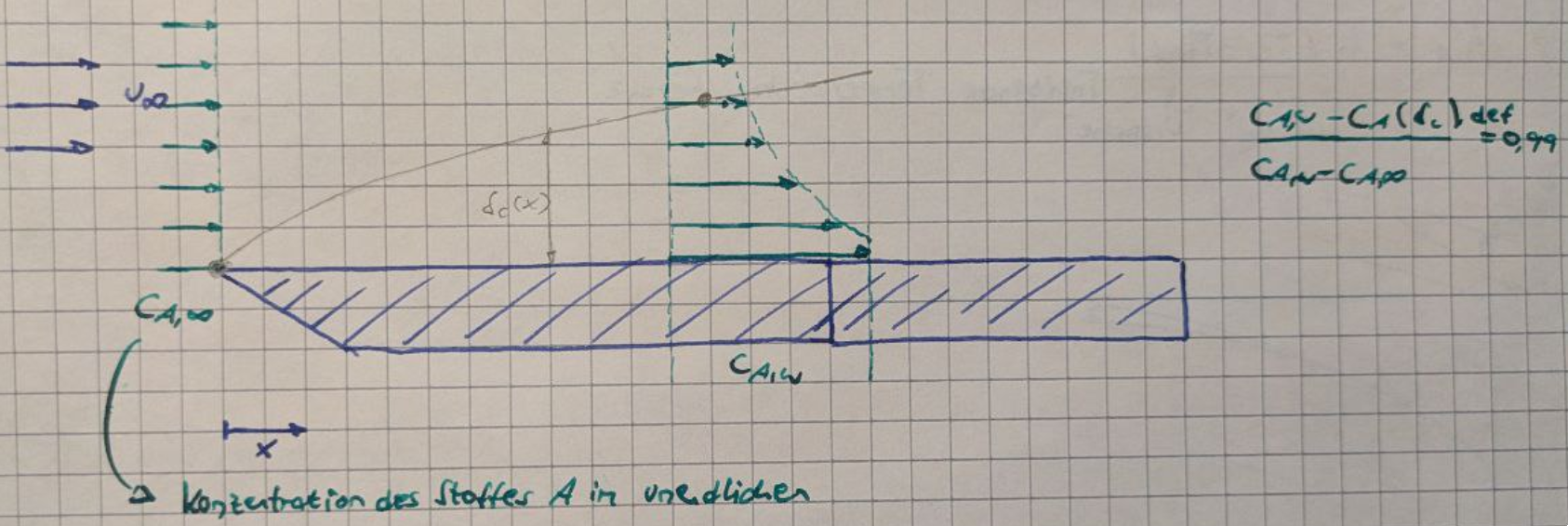
Strömungsgrenzschicht

Thermische Grenzschicht

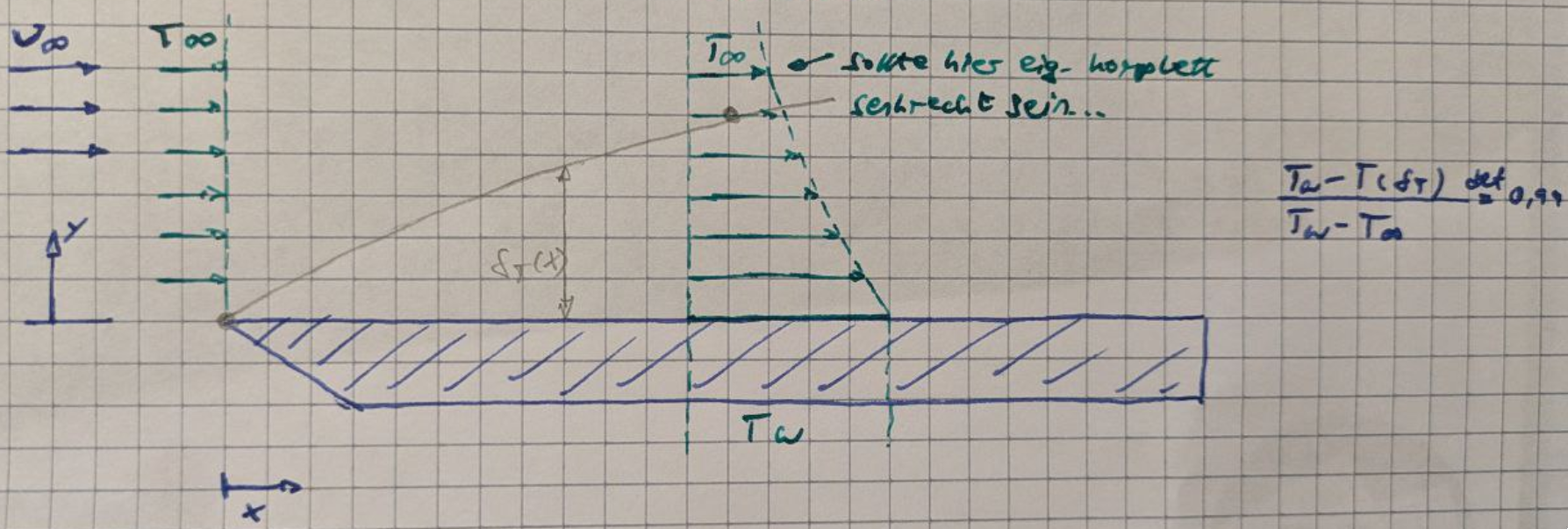
Thermische- und Konzentrationsgrenzschicht sind ähnlich, kann zum Beispiel für die naphthalene sublimation technique genutzt werden

Fourierscher Erfahrungssatz an der Wand, auf der Fluid-Seite (Keine Teilchenbewegung)

$$ \dot{q}_A = - k_f \frac{dT_f}{dy}\bigg|_{y=0^+} $$

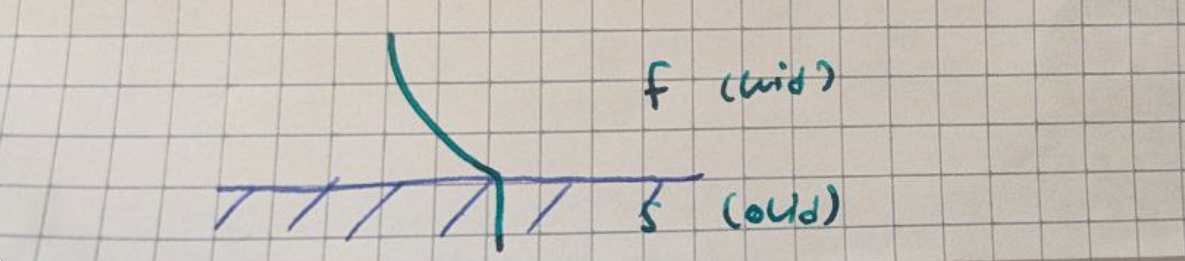
Anwendbar, da wir keine Fluidbewegungen direkt an der Wand haben\ $\rightarrow$ Wärmeleitung

Problem: Bestimmung des Gradienten, weil die Grenzschicht im Fluid so klein ist, daher Lösung über Newton mit Wärmeübergangskoeffizient $h$

Newton's Law of Cooling

$$ \dot{q}_A = h (T_w - T_\infty) $$

Problem: Die gesamten Eigenschaften der Grenzschicht sind in $h$ enthalten, es muss also für jeden Fall neu bestimmt werden, was nicht sehr einfach ist

Gleichsetzen der beiden Funktionen ergibt:

$$ h (T_w - T_\infty) = - k_f \frac{dT_f}{dy}\bigg|_{y=0^+} $$

Wärmeübergangskoeffizient

Ort der Messung der Referenztemperatur ist sehr wichtig und sollte bei Messungen festgehalten werden

Referenztemperatur

$T_{ref}$ ist beliebig wählbar, solange $\Theta_f = \frac{T_f-T_w}{T_{ref}-T_w}$ ähnlich ist
$\Theta_f$ ist bei $T_{ref}$ 1, eine Änderung von $\Theta_f$ sollte möglichst ähnlich sein, sodass die Bedeutung im Experiment und Original für $T_{ref}$ gleich ist