Flugzeugaerodynamik - Vorlesung
03 February 2026, Thorsten Lutz
| Pradtlsche Integralgleichung | Reihenansatz | |
|---|---|---|
| Entwurfsproblem | Integration | Summation |
| Nachrechenproblem | Integralgleichung | LAS - Multhopp Verfahren |
Anmerkungen zum induzierten Wiederstand
Frage: Welcher Grundriss gibt bei vorgegebener Spannweite und Auftrieb den geringsten Wiederstand (in Newton)
$$ b_I = b_{II} = b $$ $$ A_I = A_{II} = A $$ $$ k_I = k_{II} = k $$
(Annahme in Wirklichkeit nicht ganz korrekt, es wäre $k_I > k_{II}$)
Unter diesen Voraussetzungen ist der induzierte Wiederstand beider Flügel trotz unterschiedlicher Streckung gleich
Reibungswiederstand ist aber bei dem Flügel mit größerer Streckung geringer (bei geltenden Annahmen)
Induzierter Wiederstand lässt sich gut über die Erhöhung der Spannweite reduzieren, nicht aber über die verringerung der Tiefe
Winglets
- Reduziert den Gradienten der gebundenen Zirkulation an der Flügelspitze, damit die Wirbelstärke im Nachlauf und schließlich den induzierten Abwind und somit den induzierten Wiederstand gegenüber einem planaren Flügel
- Hierdurch wird die effektive Spannweite vergrößert
- Vorteil ist niedrigerer $k$-Faktor bei höheren $c_a$-Werten (Mehr Auftrieb, bzw. weniger induzierter Wiederstand bei gegebener Spannweite)
- Nachteile sind höhere Lasten am Außenflügel, damit größeres Wurzelbiegemoment (aber weniger als Spannweitenvergrößerung) und höherer Wiederstand im Schnellflug (höherer Prfilwiederstand wegen größerer umspülter Oberfläche)
Bestimmung von Roll- und Giermoment
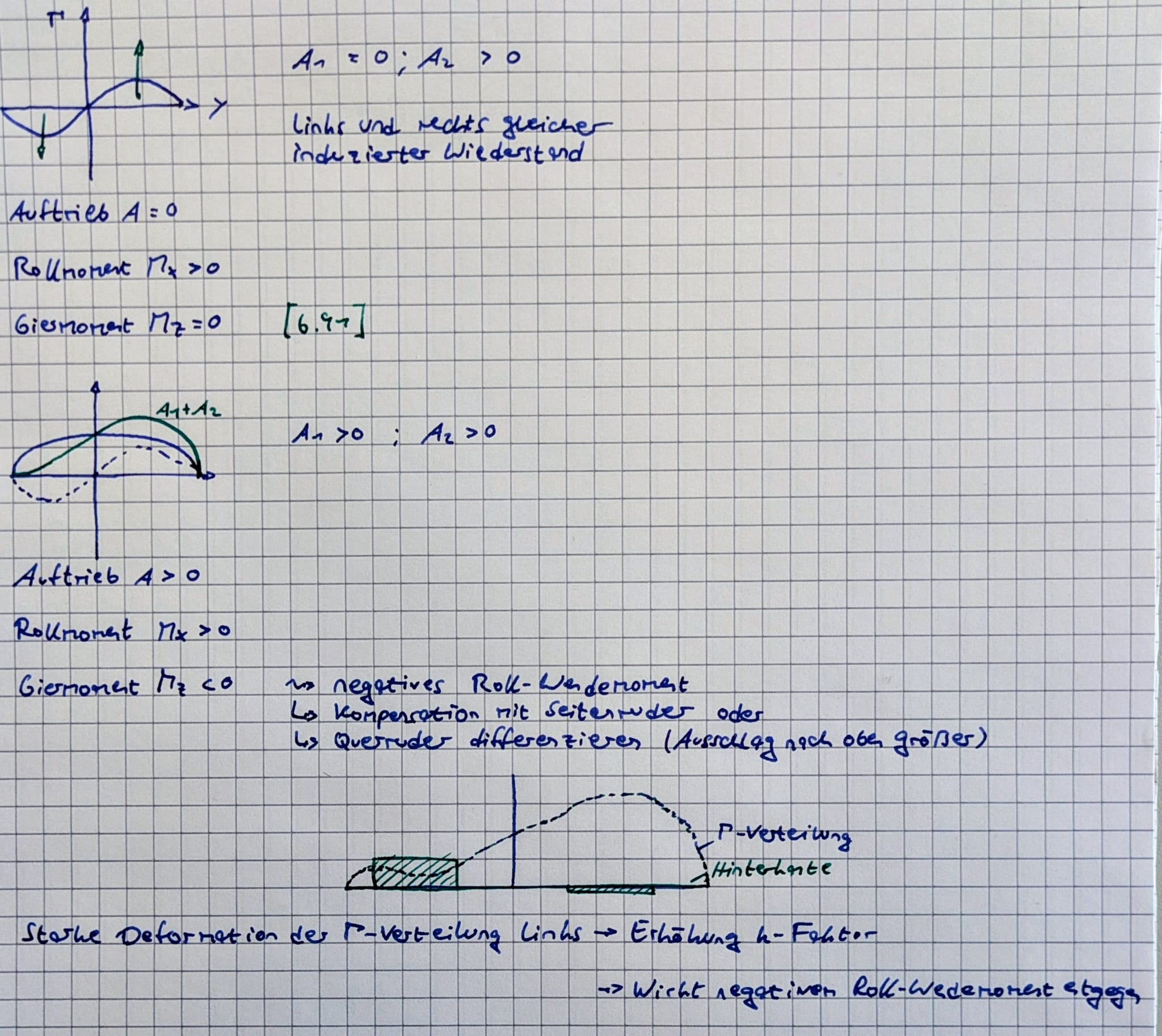
Induzierter Wiederstand ist an den Auftrieb gekoppelt, hier hat rechte Flügelhälfte mehr Auftrieb, erzeugt also auch mehr induzierten Wiederstand - Das Rollmoment macht den Unterschied, lässt sich über Erhöhung des $k$-Faktors auf der linken seite etwas kompensieren
Das Quadraturverfahren von Multhopp
Lösungsverfahren zur Lösung des Nachrechenproblems der Prandtlschen Tragliniengleichung
Lösung der Nachrechenaufgabe in folgenden Schritten:
- Berechnung der Diagonalelemente $b_v$ der Matrix $[b]$
- Aufstellen der Matrix $[b]$ unter Verwendung aller berechneten Werte $b_v$ und der Koeffizienten $b_{v\mu}$
- Vorgabe der rechten Seite des LGS
- Lösen des LGS liefert die dimensionslose Zirkulationsstärken $\gamma_{\mu}$ an den $M$ diskreten Stützstellen
- Gegebenenfalls Bestimmung der Kraftbeiwerte
Infos zur Klausur
- Fragen 45 min (Aero und Entwurf)
- Keine Hilfsmittel
- Verständnisfragen
- Aufgaben 75 min (Aero und Entwurf)
- Alle Hilfsmittel außer Altklausuren Musterlösungen
- Prüfungsvorbereitungsseminar ca. eine Woche vor der Klausur
- Weg zur Lösung muss nachvollziehbar sein
- Programmierbarer Taschenrechner sinnvoll