Flugzeugaerodynamik - Vorlesung
09 December 2025, Thorsten Lutz
Wiederholung aus letzter Stunde: Ähnlichkeitsregeln
Gödhert-Regel für kompressiblen Unterscchall
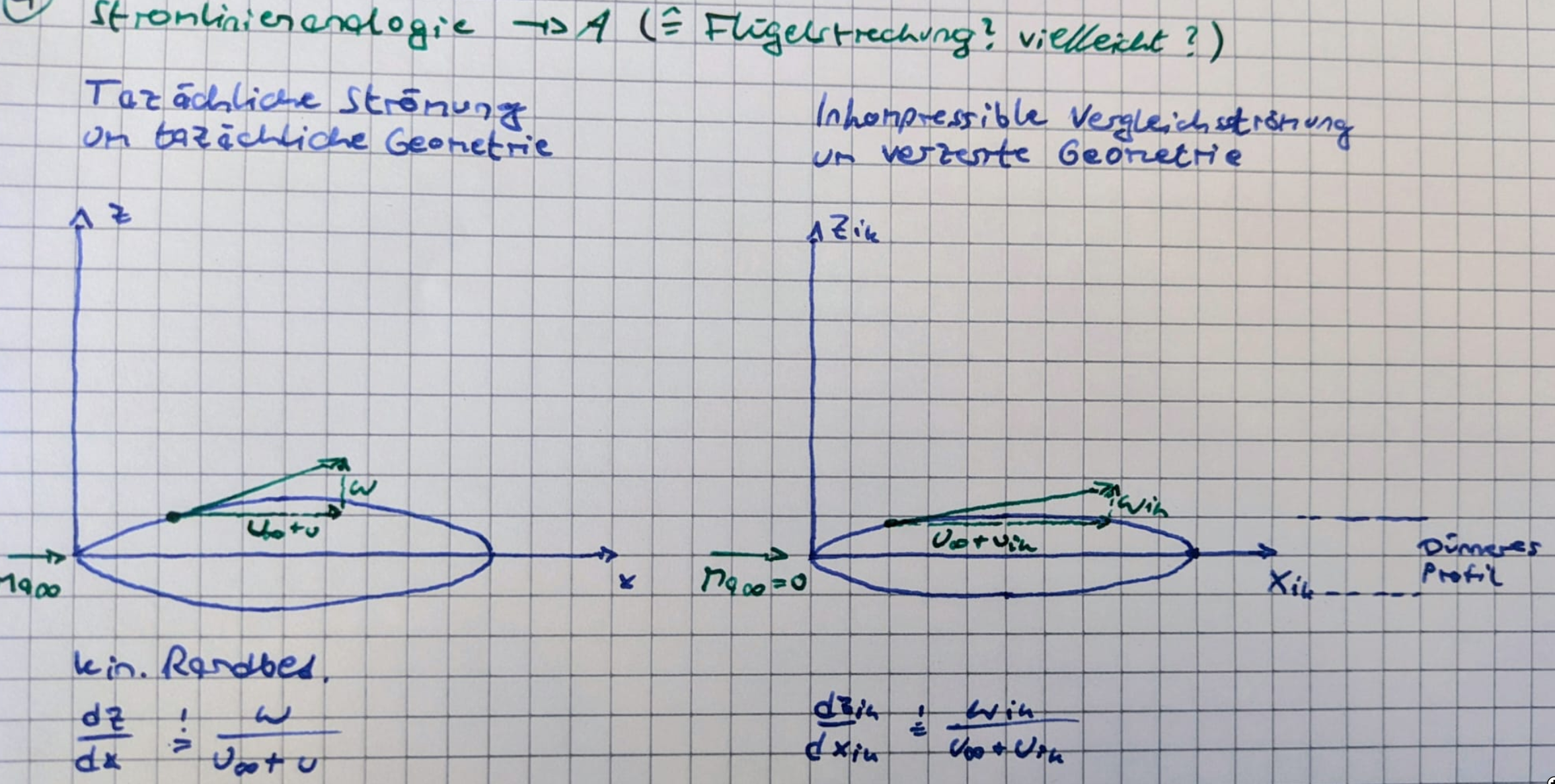
- Verzerrung der tazächlichen Geomietrie als $f(Ma_\infty)$ - 1. Prandtl-Glauert-Regel (gilt nur für 2D)
- Berechnung der inkompressiblen Vergleichsströmung ($ik$) für die verzerrte Geometrie - Lösung der Laplace Gleichung
- Dadurch erhält man $c_{a,ik}, c_{p,ik}, c_{m,ik}$
- Transformation der resultierenden Beiwerte als $f(Ma_\infty)$ - 2. Prandtl-Glauert-Regel (gilt nur für 2D)
- Daraus erhält man die gesuchten $c_a, c_p, c_m$ der tazächlichen Geometrie bei $Ma_\infty$
$\rightarrow$ Göthert Regel, ist für 3D Geometrien exakt gültig
Berechnung eines subsonisch umströmten Körpers mit der Göthert-Regel ist auf Folie 127 gut aufgeführt
Die Prandtl-Glauert Regeln
Annahme: $c_p \sim z, \alpha, f, d \rightarrow$ gilt für 2D
- Prandtl-Glauert-Regel (unveränderte Geometrie): Gleichungen 4.23 bis 4.28 im Skript $$ c_p(x,z,\alpha,f,\delta) ) \frac{1}{\beta} c_{p,ik}(x,z,\alpha,f,\delta) $$
- Prandtl-Glauert-Regel (unveränderte Druckverteilung) Gleichungen 4.29 bis 4.34 im Skript $$ c_p(x,z,\alpha,f,\delta) ) c_{p,ik}(x,\frac{1}{\beta}z,\frac{1}{\beta}\alpha,\frac{1}{\beta}f,\frac{1}{\beta}\delta) $$
Ende der Vorlesung: Beispiele zur Anwendung der Ähnlichkeitsregeln ab Folie 137