Flugzeugaerodynamik - Vorlesung

04 December 2025, Thorsten Lutz

3. Linearisierte Potenzialgleichung

Wie wirkt sich Geschwindigkeit auf den Auftrieb aus?

Vollständige Potenzialgleichung im Skript Gleichung 3.6 (gilt für homentrope, homenthalpe und drehungsfreie Strömungen)

homentrop bedeutet entropie ist im gesamten Strömungsfeld konstant, wären isentrop sich nur auf eine Stromlinie bezieht

Anwendungsgrenzen

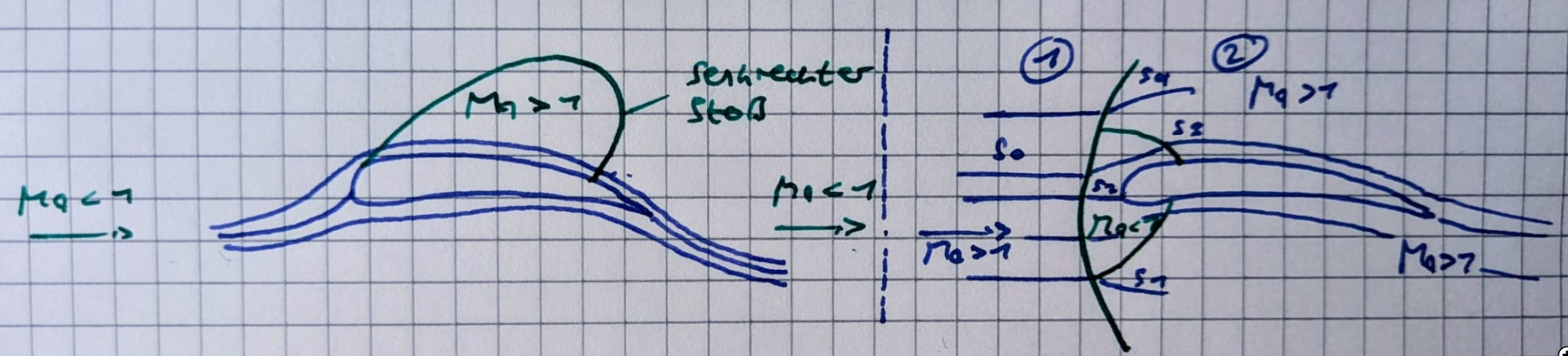
Unterschall, $Ma_\infty < 1$
- Potenzialfunktion anwendbar bis $Ma_{\text{vor Stoß}} \leq 1,3$
Überscall, $Ma_\infty > 1$
- (1) s, h = const, (homentrop, homenthalp)
- (2) $s_1 > s_2 > s_3$, aber const. entlang einzelner Stromlinien
- Entropiegradient quer zu Stromlinien - drehungsbehaftete Strömung (nach cocco)
- Potenzialfunktion nicht anwendbar

Anwendungsgrenzen der Potenzialfunktion

Vollständige Potenzialgleichung (beschreibt kompressible, homentrope, homenthalpe, drehungsfreie Strömungen)
Anwendbar im Bereich unter und knapp um $Ma \approx 1$, aber keine starken Verdichtungsstöße, abgehobenen Kopfwellen\

$\Phi$: Gesamtpotenzial, $\frac{\partial \Phi}{\partial x} = U = U_\infty + u$
$\varphi$: Störpotenzial, $\frac{\partial \varphi}{\partial x} = u$

Bei konstanter Dichte erhält man die lineare Potenzialgleichung oder die Laplace-Gleichung (inkompressibele, drehungsfreie Strömungen)
Anwenbar bei $Ma \approx 0$

Bei kleiner Strömung ($,v,w << U_\infty$) erhält man die linearisierte Potenzialgleichung (nicht verwechseln) (kompressible, drehungsfreie Strömungen)
Anwendbar bei $Ma < 1$ (subsonisch) oder $Ma > 1$ (supersonisch), nicht transsonisch
Störungen müssen klein sein, wie bei schlanken, wenig angestellten Körpern
Bereich schallnaher und hypersonischer Strömungen ist ausgenommen

Gleichungen generell leichter zu lösen, wenn Anströmung parallel zur x-Achse liegt

Der Druckbeiwert in linearisierter Form

Ähnlichkeitsregeln (subsonische Strömung)

Verzerrung der tazächlichen Geomietrie als $f(Ma_\infty)$ - 1. Prandtl-Glauert-Regel (gilt nur für 2D)
Berechnung der inkompressiblen Vergleichsströmung ($ik$) für die verzerrte Geometrie - *Lösung der Laplace Gleichung
Dadurch erhält man $c_{a,ik}, c_{p,ik}, c_{m,ik}$
Transformation der resultierenden Beiwerte als $f(Ma_\infty)$ - 2. Prandtl-Glauert-Regel (gilt nur für 2D)
Daraus erhält man die gesuchten $c_a, c_p, c_m$ der tazächlichen Geometrie bei $Ma_\infty$

$\rightarrow$ Göthert Regel, ist für 3D Geometrien exakt gültig