Flugzeugaerodynamik - Vorlesung

16 October 2025, Thorsten Lutz

Wann können wir in der aerodynamik eine Strömung als inkompressibel betrachten?

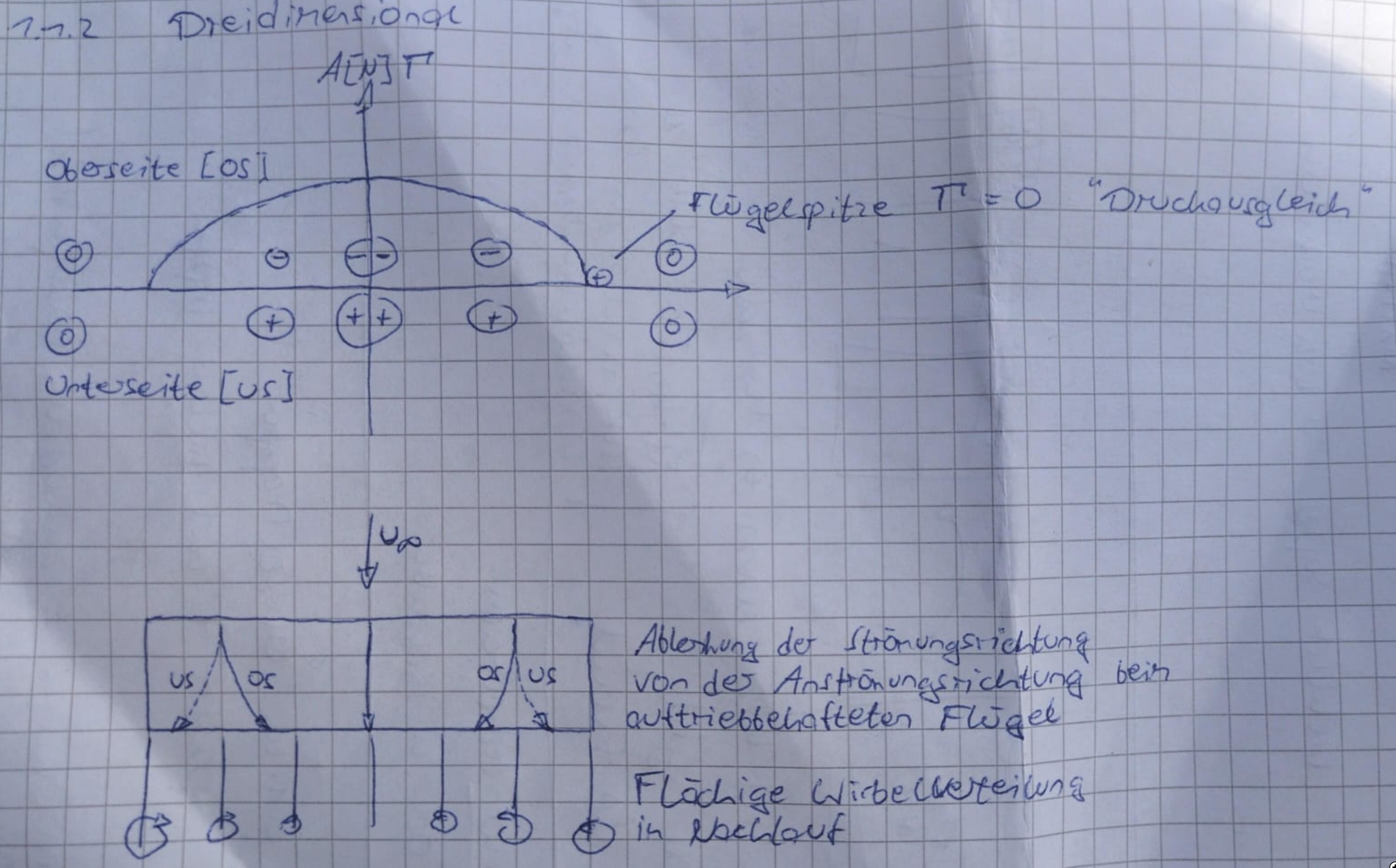
$\Lambda$ heißt mittlere Streckung

• Harte Randbedingung: Auftrieb an Flügelspitze ist immer $0$

1.2.1 Imkompressible Strömung

Bei inkompressiblen Strömungen gilt $\rho = const. \text{und} Ma_{\inf} = 0$

$$ Ma_{\infty} = 0.14 \rightarrow \frac{\rho_{staupunkt}-\rho_{\infty}}{\rho_{\infty}} = 0,01 = 1 1\% $$

$$ (\text{Luft mit} \kappa = 1,4) $$

Wir können bis zu einer Machzahl von 0,3 eine Strömung als Inkompressibel betrachten (Auch in der Klausur!)
Größte Dichteänderung passiert vom Staupunkt zur dicksten Stelle des Profils ($Ma_{max}$), nicht von vor dem Profil ($Ma_{\inf}$) zum Staupunkt

$\rightarrow$ Störungen wirken sich im gesamten Strömungsfeld aus

1.2.2 Subsonische Strömung

$$Ma_{\text{lokal}} < 1, \text{Faustregel} 0.3 \leq Ma_{\infty} \leq 0.7$$

Auftriebsbeiwert

• Reiseflug ca. 0.5 - 0.6
• Landung ca. 3

1.2.3 Transsonische Strömung

$$ Ma_{lokal} \leq 1, \text{Fausregel}: 0,7 \leq Ma_{\infty} \leq 1,3 $$