Organisation - Dimensionsanalyse

21 July 2025, Simon Volker

Begriffe

• Physikalische Größen: messbare / quantifizierbare Merkmale oder Eigenschaften von Objekten
  • Breite
  • Länge
  • Reynoldszahl
• Größenarten: qualitative Eigenschaften einer physikalischen Größe
  • Dauer -> Zeit
  • Entfernung -> Länge
• Basisgrößen: Größenarten, die voneinander unabhängig sind
• Basisgrößensystem: Gesamtheit aller Basisgrößen (es gibt 7)
  • $L$ Länge
  • $M$ Masse
  • $T$ Zeit
  • $\Theta$ Temperatur
  • $I$ Stromstärke
  • $J$ Lichtstärke
  • $N$ Stoffmenge

Ausnahmen: Winkel und Räumliche Winkel - werden in der Regel als dimensionslos betrachtet
In nicht klassisch physikalischen Problemen sind die Größen im Basisgrößensystem nicht mehr zwingend voneinander unabhängig. Beispiel $E = mc^2$

• Abgeleitete Größen: alle Größen, die aus Basisgrößen Abgeleitet werden
  • Dichte
  • Geschwindigkeit
  • Energie
  • ...
• Dimension: ist die Zuordnung zwischen einer physikalischen Größe und der Größenart
  • $[h] = L$
  • $[u] = LT^{-1}$
• Dimensionsformel: "Bridgeman Gleichung" $[x] = \prod_{i=1}^m X_i^{ai}$
  • $[x]$ physikalische Größe
  • $X_i$ i-te Basisgröße
  • $^{ai}$ Dimensionsexponent
  • $[x] = L^{a1} u^{a2} T^{a3} \Theta^{a4} I^{a5} N^{a6} J^{a7}$
  • x ist dimensionslos, wenn $a_i = 0$ für alle $i = 1,...m$
• Quantitative Beschreibung einer physikalischen Größe: Zahlenwert x Einheit
  • ${u} = m/s$
• Basiseinheiten: Einheiten der Basisgröße
  • Seit 1960: SI Einheiten
    • $L$ - m - Meter
    • $M$ - kg - Kilogram
    • $T$ - s - Sekunde
    • $\Theta$ - K - Kelvin
    • $I$ - A - Ampere
    • $N$ - mol - Mol
    • $J$ - cd - Candela

• Physikalische Gleichungen: alle Terme (alle Summanden) müssen dimensionshomogen sein

Buckinghamsches $\Pi$-Theorem

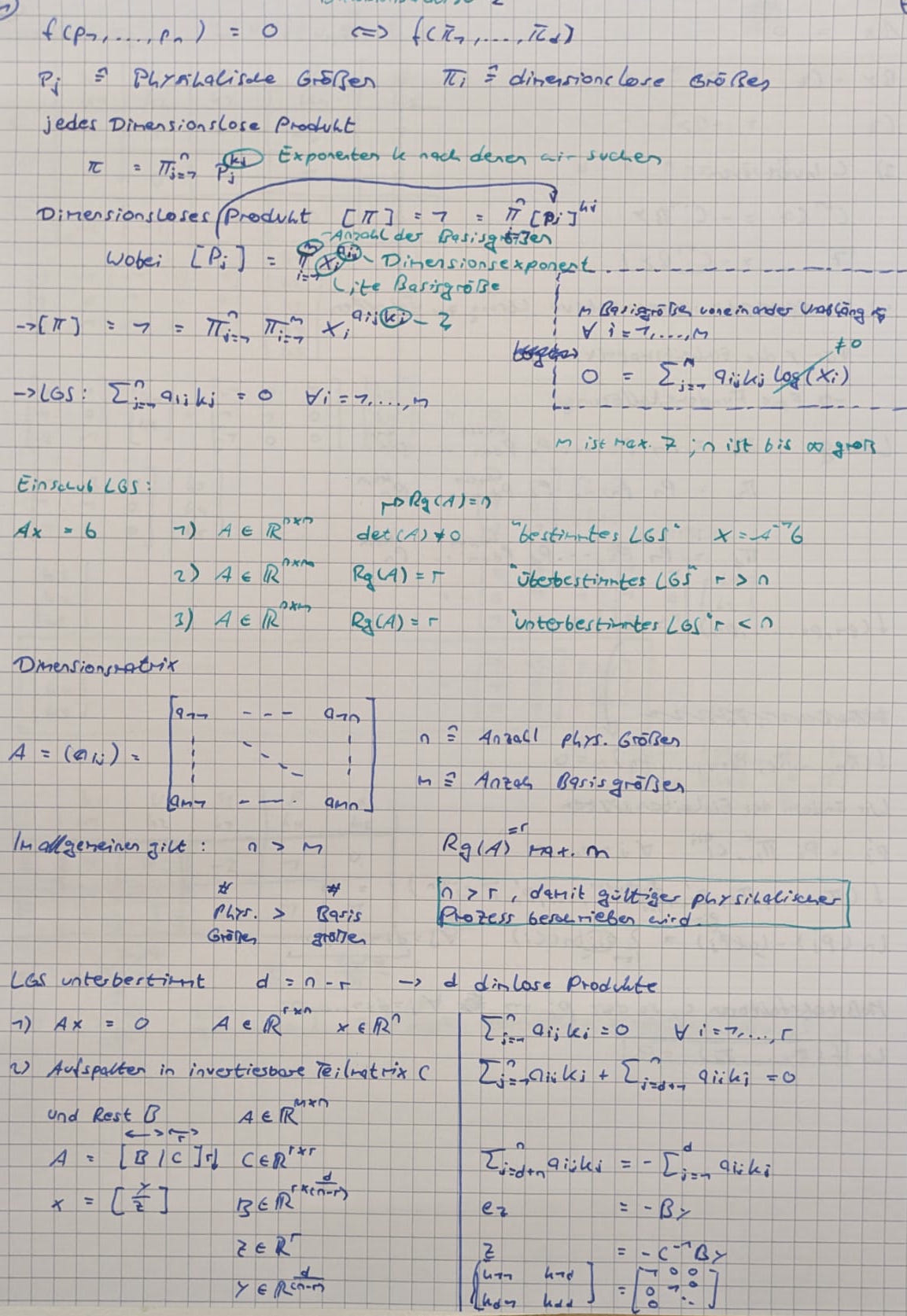
Erste Beispielrechnung

Wahl des Basisgrößensystems

Bislang [LMT] - System verwendet

$$d = n - r$$

Das [LMFT] - System
F: Einführung als eigene Basisgröße für die Kraft F

Welchen Einfluss hat die Einführung einer neuen Basisgröße?

im [LMT] - System gilt $F = m a$

Kurzzusammenfassung Wechsel des Basisgrößensystems:

• Formel des Pi Theorems ist universell - Einführung einer neuen Größe geht mit der Einführung einer Dimensionsbehafteten Konstante einher
• Ohne diese Konstante: Bruch eines grundliegenden Physikalischen Phänomens - Hat eine Implikation auf ob ein physikalischer Effekt vernachlässigt wird oder nicht.