Analytische und Numerische Methoden - Numerik

10 July 2025, Andrea Beck

Berechnung des Numerischen Flusses

$$g_{i+\frac{1}{2}}^n = g\left(u_i^n, u_{i+1}^n\right) \quad \text{heißt numerischer Fluss und approximiert} \quad \frac{1}{\Delta t} \int_{t_n}^{t_{n+1}} f\left(u\left(x_{i+\frac{1}{2}}, t\right)\right) dt$$

Sollten sie schonmal gehört haben: "Flussvekotr-Splitting-Form"
Weitere Möglichkeit den Fluss aufzischreiben ist die "Flussdifferenz-Splitting Form" (Diese Form ist nur so zur Info)

Wie klein muss der Zeitschritt sein?

$$\Delta t < \frac{\Delta x}{|a|} \quad \text{oder} \quad \frac{\Delta t}{\Delta x} |a| < 1$$

Information darf in einem Zeitschritt nur durch eine Gitterzelle laufen.
Dies war die Schrittweitenbedingung bei dem Upwind-Differenzen-Verfahren (CFL-Bedingung), welches die Stabilität garantiert. Hier ist es eine Konsistenzbedingung
Das Einflussgebiet des numerischen Vefahrens muss das der exakten Lösung überdecken

Lösung des Riemannproblems für die Lineare Wellengleichung

Beispiel 11.4 in den Vorlesungsfolien

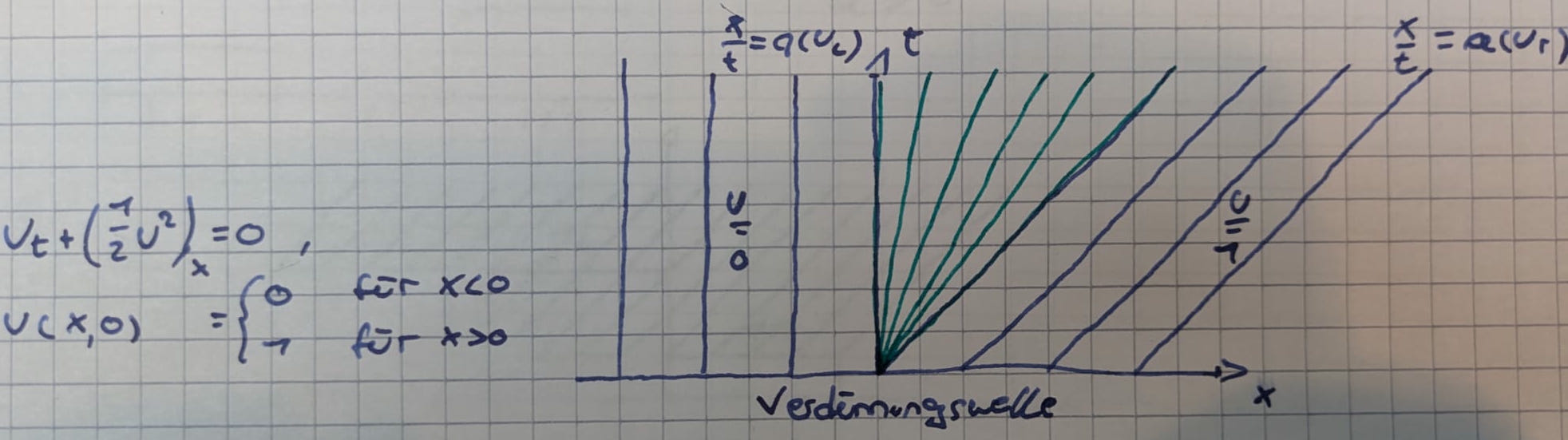
Wo kommt noch die fehlende Information her?

1. Integrale Erhaltung - Im Stoßfall ergibt sich die Rankine-Hugoniot Bedingung aus der integralen Erhaltung. Die integrale Erhaltung bestimmt die Stoßgeschwindigkeit
2. Entropiebedingung - Die Entropiebedingung bestimmt, dass es im Verdünnungs- fall die stetige Lösung genommen wird und kein Verdünnungs- stoß auftritt.

Systeme von Erhaltungsgleichungen (z.B. Navier-Stokes)

Quasilineare Form der Funktion kann aufgestellt werden, Problem ist aber, dass diese Gleichung nicht mehr entkoppelt werden kann. Beim LInearen System würde als nächstes mit Hauptachsentransformation entkoppelt werden. Funktionert jetzt nicht, weil Eigenwerte nicht mehr konstant, sondern Funktionen der Lösung $u$ sind. (Folie 57)

Keine Rechenaufgabe zu Kapitel 11.2.4 in der Klausur

Bis Folie 79 gekommen, der rest nicht in der Klausur