Analytische und Numerische Methoden - Numerik

08 July 2025, Andrea Beck

Finite Volumen Verfahren in einer Raumdimension

Der wesentliche Baustein eines Finite Volumen Verfahrens ist die Berechnung des numerischen Flusses.

Schwierigkeit; Nur die integralen Mittelwerte sind verfügbar

Einfachste Idee: Arithmetischer Mittelwert des Flusses ausgewertet an den Mittelwerten zum alten Zeitpunkt

$$g^n_{i+1/2} := \frac{1}{2}(f(u^n_i)+f(u^n_{i+1}))$$

Oben eingesetzt ergibt dies die gleiche Gleichung wie bei einem Differenzen-Verfahren mit zentralen Differenzen im Raum und der expliziten Zeitapproximation erster Ordnung $\rightarrow$ instabil

Godunovs Idee

Konstante Zustände $u$ in den Zellen, aber unstetig an den Zellgrenzen

Godunovs Beobachtung

Das entspricht gerade dem sogenannten „Riemann Problem“, für das man analytische Lösungen bestimmen kann

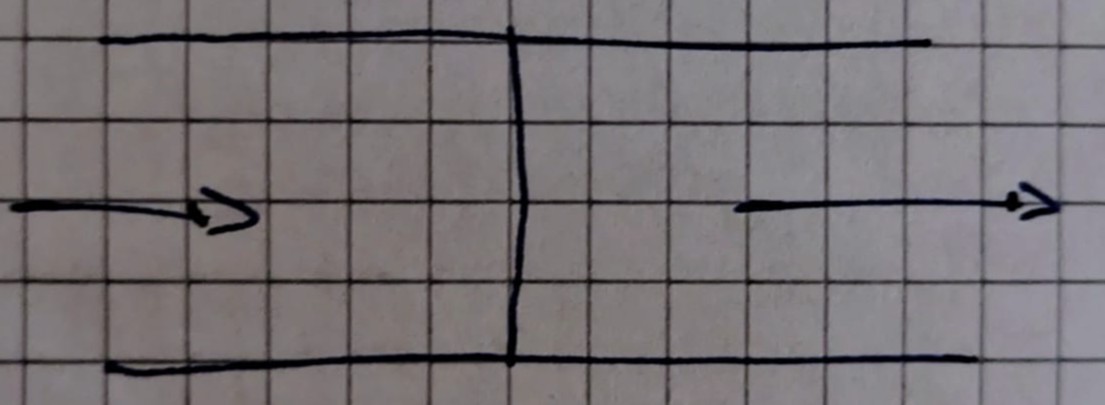
Die Lösung besteht aus m + 1 konstanten Zuständen, welche durch m Charakteristiken getrennt werden

Was bedeutet die Zeichnung mit den Charakteristiken Folie 35? Was nimmt ein Beobachter war? In jedem Punkt im Raum Zeit kontinuum - welcher Punkt / Zustand existiert dort gerade?

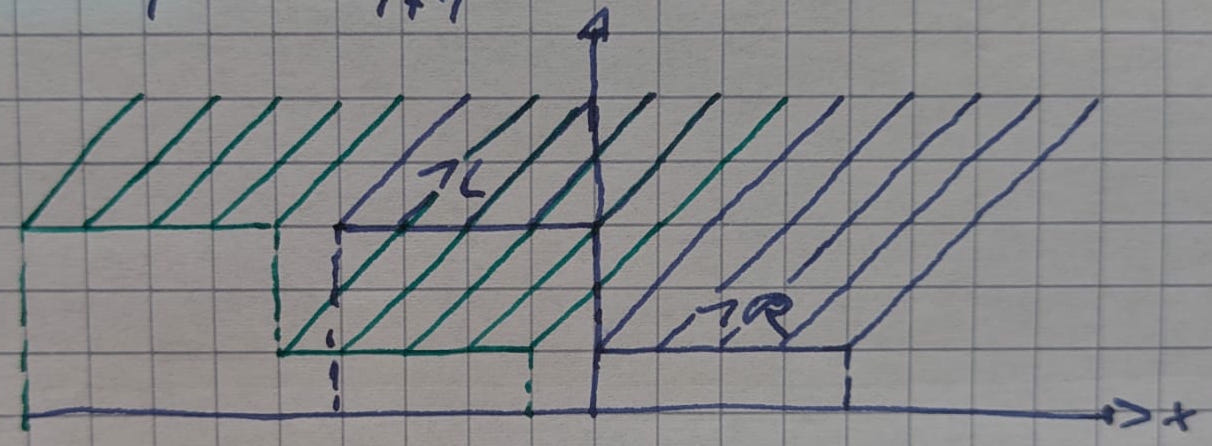
Entlang der Charakteristik transportiert sich die Information über den Zustand der Lösung Wie schaut die Lösung an einem Punkt x im Verlauf der Zeit aus?