Analytische und Numerische Methoden - Numerik

01 July 2025, Andrea Beck

Numerische Methoden für Hyperbolische Differentialgleichungen

Zentrale Differenzenbildung ist bei hyperbolischen Dgln problematisch – insbesondere ist sie instabil in Verbindung mit expliziter Zeitappoximation 1. Ordnung

Lösung des Stabilitätsproblems

1. Möglichkeit: Man berücksichtigt das Vorzeichen der Wellenausbreitung: Upwind-Verfahren
   • Numerische Approximation genau wie die Ausbreitung auch nur aus einer Richtung beeinflusst
   • Differenzen aus Richtung- aus der die Information kommt:
2. Heute nicht mehr stark im Einsatz: Verfahren höherer Ordnung in der Zeit in Kombination mit zentralen Differenzen und Stabilisierungsterme im Raum (Künstliche Viskosität)
   • Ändern des Diskretisierungsfehlers durch dissipativen Term, welcher sich über $\epsilon$ beeinflussen lässt
3. Lax-Wendroff-Verfahren: Nicht in dieser Vorlesung behandelt, gibts aber auch noch

• Explizite Verfahren mit 1. Ordnung Zeitapproximation
• Das explizite Verfahren ist bedingungslos instabil.
• Das explizite Verfahren mit Upwind-Differenzen (CIR) ist bedingt stabil unter der CFL-Bedingung

Lineare Hyperbolische Systeme

System von hyperbolischen Differenzialgleichungen:
Die Matrix besitze einen vollständigen Satz von Eigenvektoren und ist diagonalisierbar
Verfahren mit zentralen Differenzen sind einfach übertragbar, indem man die Verfahren einfach auf jede Gleichung anwendet.

Für die CFL-Bedingung müssen alle Wellengeschwindigkeiten herangezogen werden:

(### CIR Verfahren für Charakteristische Normalform)

Der Nicht Lineare Fall

Finites Differenzen Verfahren funktioniert hier nicht so gut, kommt durch Approximation mit Poylnomen schlecht mit Sprüngen (Verdichtungsstößen) in der Lösung zurecht\

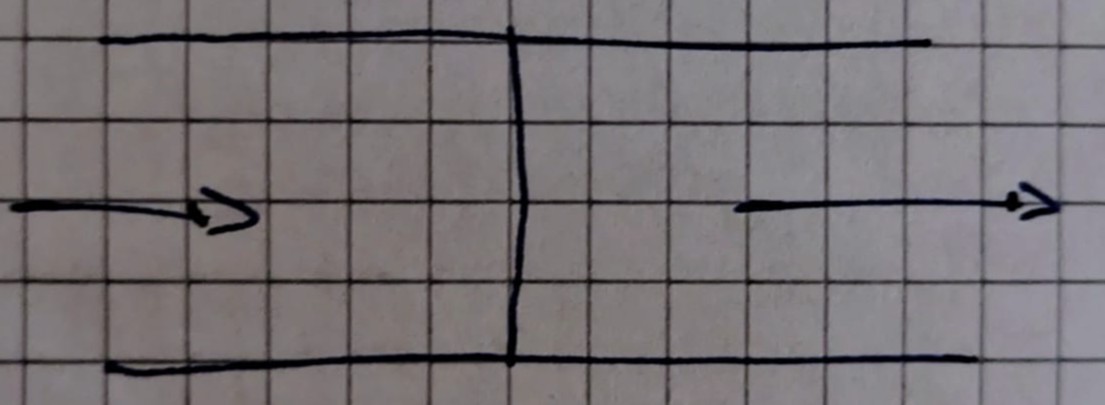
Position des Stoßes ändert sich bei Geringem Fehler in der Abschätzungen am Ein- und Auslauf (z.B. Druck) erheblich
Unterschiedliche Verteilung der Gitterpunkte am Ein- und Auslauf kann bewirken, dass die einläufenden Ströme nicht gleich den auslaufenden sind - Keine Garantie beim Finiten Differenzenverfahren
Kommt daher, dass keine Integralen Betrachtungsweisen erlaubt sind (Nicht-konversativität der Differenzenverfahren)