Analytische und Numerische Methoden - Numerik
05 June 2025, Andrea Beck
Testate
Alle Hilfsmittel sind erlaubt (Aber nicht überstrapazieren)
Erstes Testat am 18.6.
Numerische Lösung von elliptischen Differenzialgleichungen
Das Differenzenverfahren
- Schritt: Diskretisierung des Räumlichen Rechengebiets
- Schritt: Auswahö und Einsetzen der Differenzenquotienten
- Schritt: Sortieren der Differenzengleichungen
- Lösen des Gleichungssystems
Differenzenverfahren auf randangepassten Gittern
Differenzialoperator kann jetzt nicht mehr durch etwas einfacheres wie eine Sekantensteigung ersetzt werden.
Trick: Transformation des Gebiets auf Referenzgebiet: Abbildung des gekrümmten Elements (physikalisch) auf ein logisches Gebiet, in dem wir es wieder mit einem Rechteck zu tun haben.
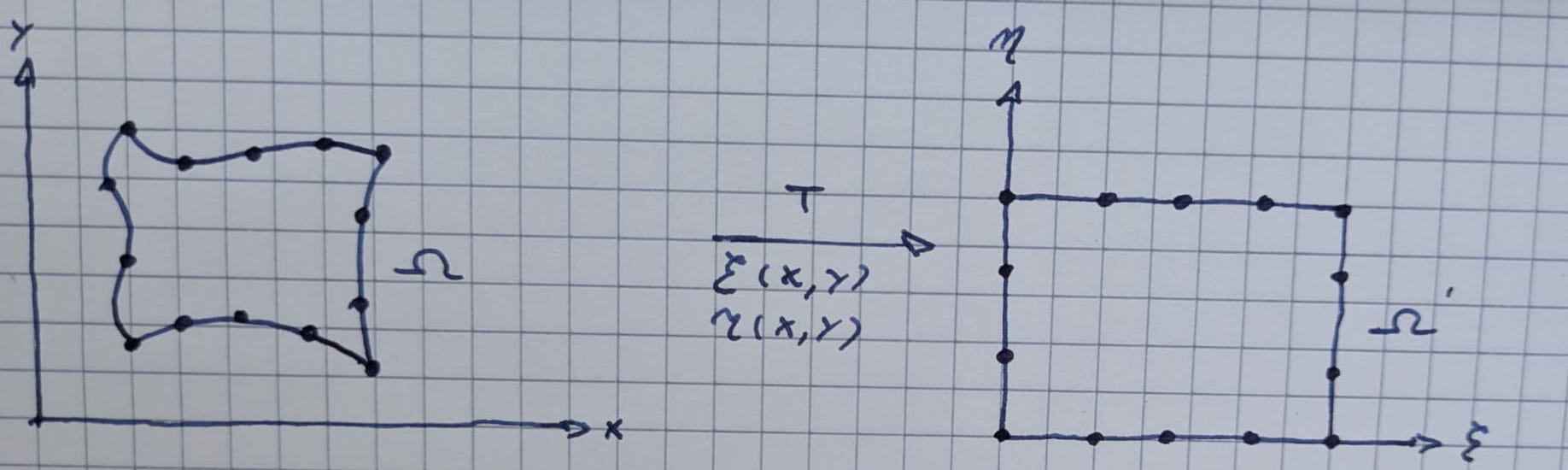
Dann lösen und wieder auf das physikalische Rechengebiet zurücktransformieren
Beispiel Ab Folie 9 (angenommen xi und eta sind bekannt)

Finite Elemente Verfahren für elliptische Gleichungen
- Schritt: Multiplikation mit einer Testfunktion und Integration
- Schritt in 2D: Partielle Integration
Das Galerkin-Verfahren: Unendliche Basis von $H^1$ durch eine endlich dimensionale Basis ersetzen, z.B. Hutfunktionen. In schwacher Formulierung kein Problem, dass die Hutfunktionen an einzelnen Punkten nicht stetig differenzierbar sind.
Basisfunktionen und lokale Steifigkeits- und Massenmatrix
Einsetzen des Ansatzes in die schwacher Formulierung und Wahl der Basisfunktionen als Testfunktionen ergibt das Galerkin-Verfahren. Vereinfachung: Alle Basisfunktionen Null auf dem Rand - homogene Dirichlet-Randwerte
$$\int_\Omega \nabla u (\underline{x}) \cdot \nabla \varphi (\underline{x}) d \Omega = - \int_\Omega f(\underline{x}) \varphi(\underline{x}) d\Omega$$