Analytische und Numerische Methoden - Numerik
22 May 2025, Andrea Beck
Die nichtlineare Wärmeleitungsgleichung
$$u_t = \nabla \cdot (\kappa(u)\nabla u)$$
Vollimplizites Verfahren
$$\frac{u^{n+1} - u^n}{\Delta t} = \tilde{\nabla} \cdot (\kappa(u^{n+1}) \tilde{\nabla} u^{n+1})$$
$$...$$
Ansatz 1: Einfache Linearisierung
damit hat man wie im linearen Fall ein lineares Gleichunngssystem erzeugt, das jetzt in jeder Iteration geößt werden muss.
Im Falle der Konvergenz wird das nichtlineare System durch die Grenzfunktion erfüllt
Start der Iteration
(Folie 18)
Anssatz 2: Fixpunktiteration - nichtlineares SOR-Verfahren
(Folie 19)
Ansatz 3: Newton-Verfahren
(Folie 21)
Galerkin-Verfahren
Herleitung der schwachen Form - Lösung soll normal auf dem Testraum stehen, sie soll das gleiche Integral wie die Ursprungsfunktion haben, nicht exakt identisch sein (Siehe Foto mitschrieb von Folie 25)
- Multiplikation der DGL mit einer Testfunktion $v(x)$
- Integration über das Rechengebiet
- Partielle Integration
schwache Formulierung der Wärmeleitungsgleichung
$$\int_a^b { u_t v + \kappa u_x v_x } , dx - [\kappa u_x v ]_a^b = \int_a^b f v dx$$
Mathematisch ist schwache Form identisch zu starker Form\
- Etwas allgemeinere Formulierung des physikalischen Problems
- Mit schwächeren RegularitätsVoraussetzungen
- Annahme, dass die Testfunktion nur von der Raumvariablen $x$ abhängt
Approximation
Man betrachtet jetzt nicht den gesamten Lösungsraum, sondern gibt eine Häherungslösung als Linearkombination von einer endlichen Anzahl von Basisfunktionen vor:
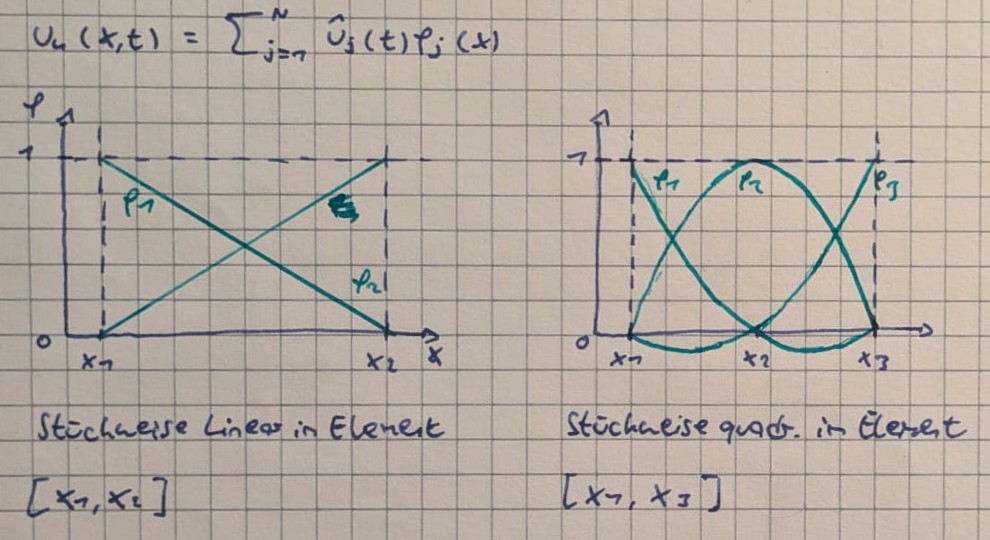
$$u_h(x,t) = \sum_{j=1}^N \hat{u}_j(t) \varphi_j(x)$$
$u_h(x,t)$ - Ansatzfunktion
$t$ - Freiheitsgrade
$\varphi_j$ - Basis- oder Formfunktion
Die Näherungsfunktion wird in die schwache Formulierung eingesetzt
Galerkin Ansatz: Testfunktion gleich der Basisfunktionen wählen
Linienmethods: Aufteilen in Räumliche und Zeitliche Anteile
Einfache Zeitdiskretisierungen: Explizites Euler-Cauchy-Verfahren
Im Unterschied zu den Differenzen-Verfahren benötigen FR-Verfahren auch bei expliziter Zeitapproximation die Lösung eines Gleichunssystems
Eine Zeitschrittweitenbeschänlung zur Sicherung der Stabilität tritt auf
Bei parabolischen Problemen muss der Zeitschritt proportional zum Quadrat der Raumschrittweite gewählt werden - Meist implizite Verfahren.
Einfachstes Verfahren impliziten Euler-Verfahren, auch voll-implizites Verfahren genannt
Die hier vorgestellten impliziten Verfahren: voll-implizit, Crank-Nicolson und BDF Formeln sind bedingungslos stabil, während explizite Verfahren nur bedingt stabil sind.
Die Zeitschrittweite ist proportional des Quadrats des Raumschrittes und hängt ab von dem kleinsten Eigenwert von
$$- \underline{\underline{M}}^{-1} \underline{\underline{K}}$$
ab
Finite-Elemente
Basisfunktionen sind nur lokal aktiv. Der einfachste Fall sind die Hut-Funktionen oder Dreiecksfunktionen (Überall definiert, aber haben nur bei $x_i$ einen Wert ungleich 0) - Bewirkt dass Einträge in der Stefigkeitsmatrix $\underline{\underline{K}}$ größtenteils $0$ sind
Randbedungungen
Bislang hatten wir nur homogene Dirichlet-Randbedungungen gefordert
$$u(a, t) = 0, \quad u(b, t) = 0 \quad \text{für} \quad t > 0$$
Allgemeine Dirichlet-Randbedungungen
$$u(a, t) = g_a(t), \quad u(b, t) = g_b(t) \quad \text{für} \quad t > 0$$
- Starke Approximation der Randwerte
Idee: Die Randwerte werden in der Näherungsfunktion direkt vorgeschrieben
Dazu modifizieren wir die Approximation folgendermaßen:
- Schwache Approximation der Randwerte
Idee: Die Randwerte gehen nur in die schwache Formulierung ein - auch die Randwerte werden nur näherungsweise approximiert
Annsatzfunktionen mit zwei zusätzlichen Basisfunktionen und Testfunktionen:
Dies funktioniert auch mit Neumann-Randbedingungen
$$u(a, t) = s_a(t), \quad u(b, t) = s_b(t) \quad \text{für} \quad t > 0$$