Analytische und Numerische Methoden - Numerik
20 May 2025, Andrea Beck
Das Finite Elemente Verfahren
- Diskretisierung des Rechengebiets und Auswahl von lokalen Basisfunktionen (Folie 35)
- Einfachster Fall: stückweise linear
- Basisfunktionen sind nur lokal aktiv
- Auswahl der Methode der gewichteten Residuen (Folie 38)
- Meistens Galerkin-Verfahren
- Start mit schwacher Formulierung der DGL
- Einsetzen der Ansatzfunktion
- Aufstellen und Lösen des Gleichungssystems
Fazit
- Komplizierter als finite differenzen
- Idee: Approximation der Lösung durch einfache Funktionen
- Diese sind Linearkombination von Basisfunktionen
- Basisfunktionen nur in einer Gitterzelle und den direkten Nachbarn $\neq 0$
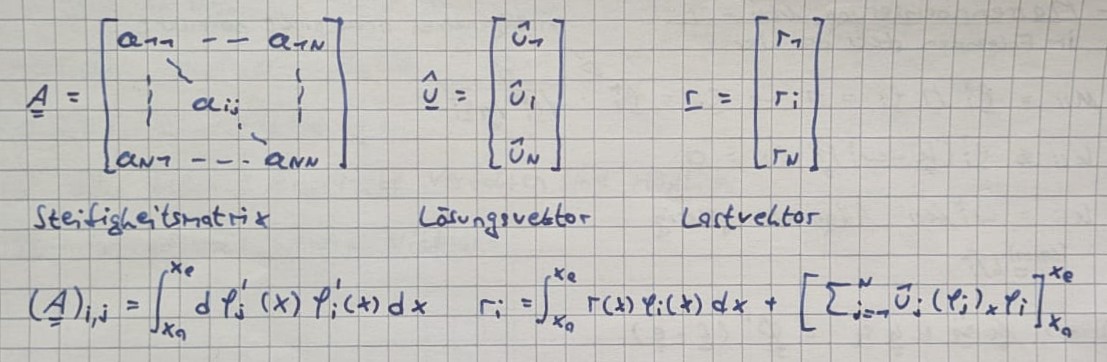
- Schwach besetzte Gleichungssysteme
- Freiheitsgrade bestimmt mit Galerkin-Verfahren
- Masse-Matrix, Steifigkeitsmatrix, ...für jede Gitterzelle bestimmen
- Assemblierung
Linienmethode
Konvektions-Diffusions-Reaktions-Gleichung
$$u_t + \underline{a} \cdot \nabla u = d \Delta u + r \quad \text{zeitabhängig}$$
$\underline{a}$ - Konvektion mit der Geschwindigkeit $\underline{a}$ hyperbolisch
$d$ - Diffusion mit dem Koeffizienten $d \geq 0$ parabolisch
$r$ - Reaktion mit dem Quellterm $r(x)$
Wir führen jetzt eine Zeitapproximation und eine Raumapproximation ein
Gleichung in zwei Raumdimensionen:
$$u_t + a_1 u_x + a_2 u_y = d (u_{xx} + u_{yy}) + r$$
An jedem Gitterpunkt $x_i, y_j$ gilt die gewöhnliche Differenzialgleichung in der Zeit
Dies gilt für jeden inneren Gitterpunkt $i = 1, \dots, n_1 - 1, \quad j = 1, \dots, n_2 - 1$
- An den Rändern physikalisch sinnvolle Randbedingungen vorgegeben
- In Gleichung oben für die Rand nahen Gitterpunkte einsetzen (Dirichletbedingungen)
- Als zusätzliche Gleichungen vorgeben (Neumann Randbedingungen)
Numerische Lösung von parabolischen Differenzialgleichungen
Lineare Wärmeleitungsgleichung
$$u_t = \kappa \Delta u \quad \text{mit} \quad \kappa \in \mathfrak{R}, \quad \kappa > 0$$
Lineare Wärmeleitungsgleichung in einer Raumdimension
$$u_t = \kappa u_{xx} \quad \text{in} \quad [a, b] \times [0, T]$$
- Explizites Verfahren mit zentralen Differenzen
- Implizittes Verfahren mit zentralen Differenzen
- Implizites Verfahren 2. Ordnung in Raum und Zeit - Crank-Nicholsen-Verfahren

Die nichtlineare Wärmeleitungsgleichung
$$u_t = \nabla \cdot (\kappa(u)\nabla u)$$
Vollimplizites Verfahren
$$\frac{u^{n+1} - u^n}{\Delta t} = \tilde{\nabla} \cdot (\kappa(u^{n+1}) \tilde{\nabla} u^{n+1})$$
$$...$$
... Dies ist ein System von nichtlinearen Gleichungen. Wie löst man diese?
Als nichtlineares Gleichungssystem: Iterativ
Welche Möglichkeiten gibt es, um eine Iterationsvorschrift zu erhalten?
- Ansatz 1: Einfache Linearisierung (Einfach nur eine Fixpunktiteration)
- Ansatz 2: Fixpunktiteration - nichtlineares SOR - Verfahren
- Ansatz 3; Newton - Verfahren