Analytische und Numerische Methoden - Analytik
13 May 2025, Bernhard Weigand
Lösung von nichtlinearen Problemen
Instationäre Wärmeleitung in einem halb-unendlichen Körper mit einer temperaturabhängigen Wärmeleitfähigkeit

Modell ist beschreibbar mit eindimensionaler instationärer Wärmeleitungsgleichung wegen $\theta$ nicht lineare DGL
Störungsrechnung
Lösungsmethode für nicht partielle gewöhnliche differentialgleichungen (nochmal im Skript nachlesen ob das so richtig ist)

Reguläre Störungsrechnung
Singuläre Störungsrechung wird nicht in dieser Vorlesung betrachtet
Störungsansatz einsetzen - man erhält eine reihe die im gesamten feld konvergiert - die gleichung ist linearisiert
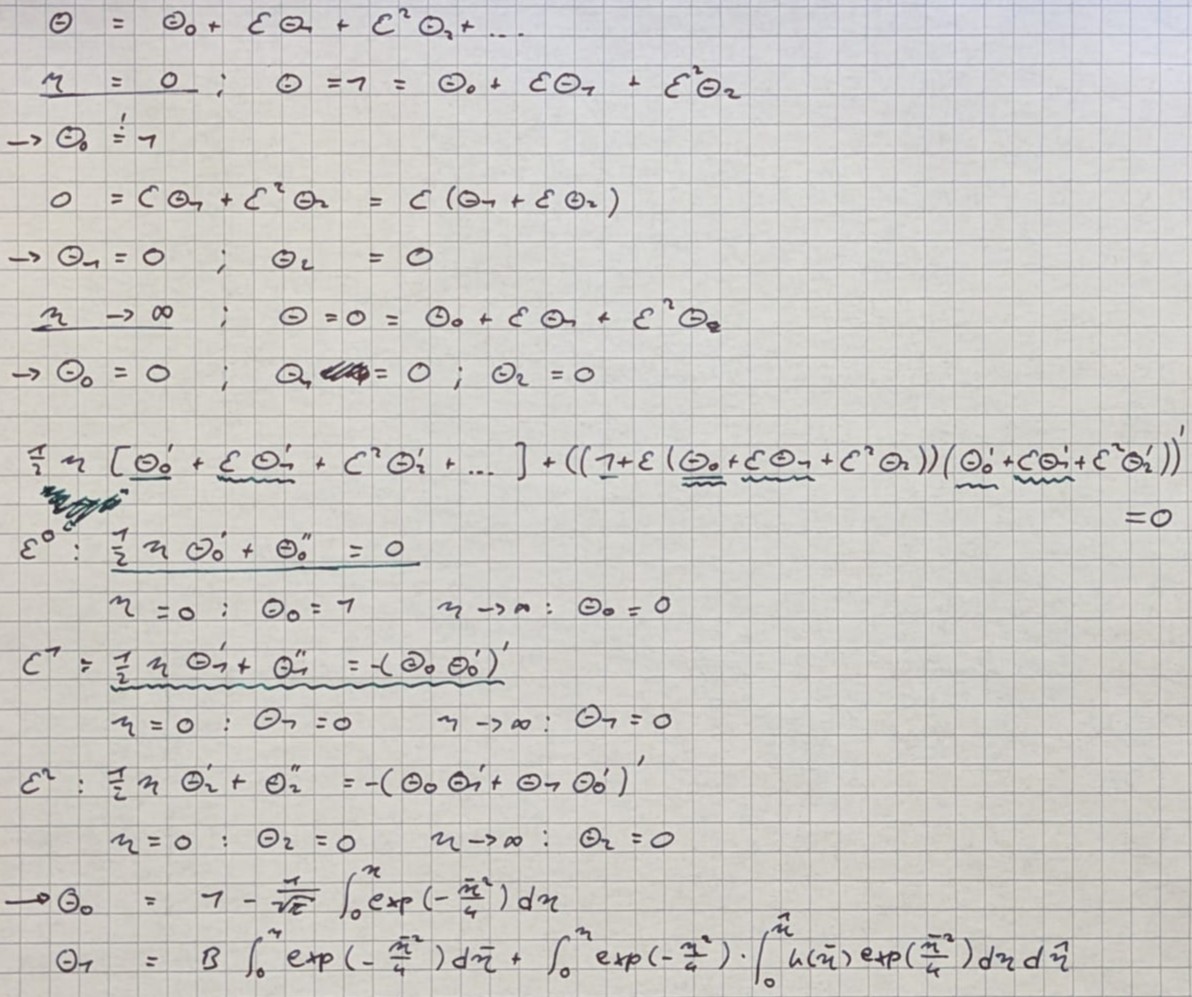
Beispiel: Strömung und Wärmeübergang über eine längsangeströmte Platte
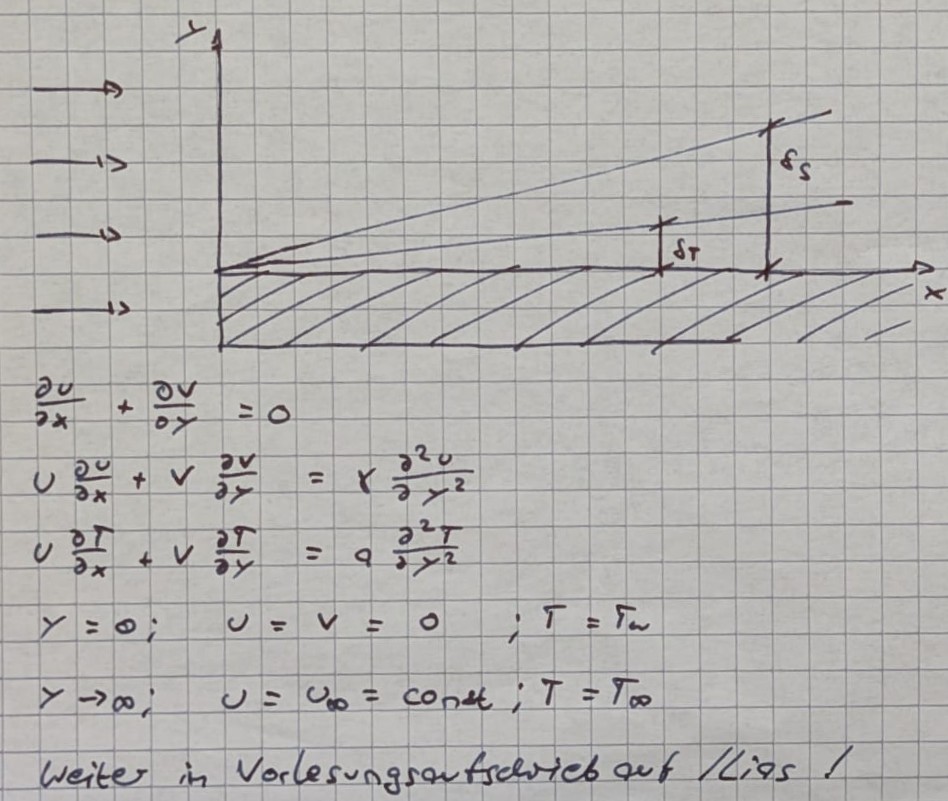
Blasiussche Gleichung
$$f''' + \frac{1}{2} f f'' = 0$$
$$f'(0) = 0 ; \qquad f(0) = 0 ; \qquad f'(\eta \rightarrow \inf) = 1$$