Analytische und Numerische Methoden - Numerik
06 May 2025, Andrea Beck
Kapitel 5 - Approximation von Differentialgleichungen
Motivation
Eine allgmeine Modellgleichung für viele physikalische Probleme ist die Konvektions-Diffusions-Gleichung


Bei der numerischen Approximation trennt man sehr gerne die Zeit- und Raumapproximation, um das Problem etwas übersichtlicher zu gestalten. Dieses Vorgehen nennt man die die Linienmethode: Getrennte Betrachtung der Zeit –und der Raumapproximation - Wir kümmern uns zunächst nur um alle Operatoren fest in der Zeit, danach wird getrennt die Zeitntwicklung betrachtet
Beispiel Folie 6
Wichtig:
Die Zeitapproximation besteht somit aus einer Lösung eines AWP, während die Raumapproximation die Lösung eines RWP darstellt.

Zeit- und Raumapproximation 5.1
Anfangswertproblem:
$$\underline{\dot{u}} = \underline{f}(t,\underline{u}) \quad \text{mit} \quad \underline{u}(0) = \underline{u}^0$$
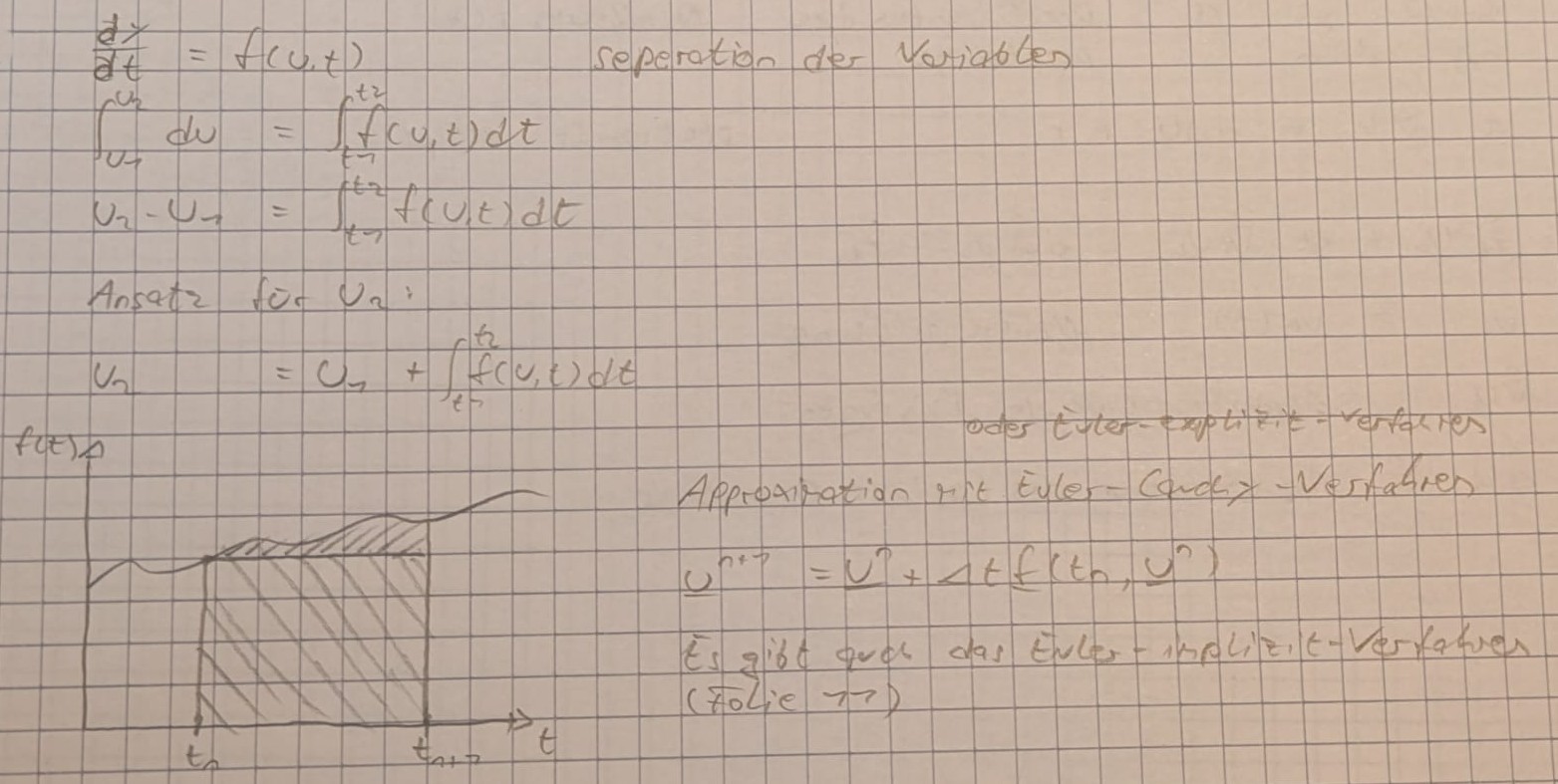
Sukzessive Integration der Dgl in der Zeit über einen Zeitschritt ergibt:
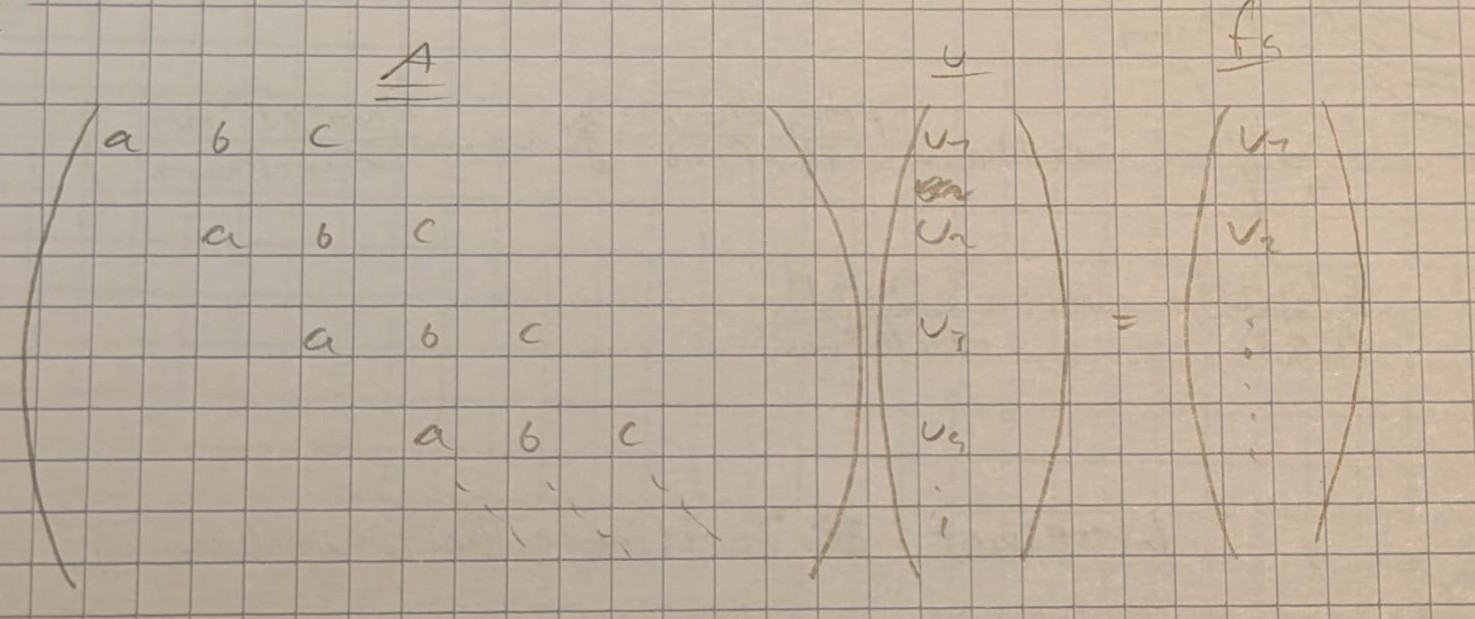
$$\underline{u} _i^{n+1} = \underline{u} _i^{n} + \int_{t_n}^{t_{n+1}} \underline{f}(t,\underline{u})dt$$
Einfachste Approximation: Euler-Cauchy-Verfahren
Anwendung der Rechteckregel:
$$\underline{u}^{n+1} = \underline{u}^n + \Delta t \underline{f}(t_n, \underline{u}^n)$$
Man befindet sicha uf dem Zeitlevel $t_n$ und greift auf den Wert des nächsten Levels $t_{n+1}$ zu
Ist die rechte Seite nichtlinear, dann muss die Lösung mit einem iterativen Verfahren bestimmt werden.
Euler-Verfahren implizit und explizit sind Verfahren 1. Ordnung (Genauigkeit verdoppelt sich mit doppelter Stützstellenzahl).
Für praktische Simulationen hat man gerne Verfahren mindestens 2. Ordnung.
Die Näherungslösung auf dem nächsten Zeitlevel lässt sich bei einem expliziten Verfahren einfach berechnen. Allerdings ist die Stabilität des Verfahrens vom Zeitschritt abhängig. Bezüglich der Wahl des Zeitschritts und der Stabilität sind die impliziten Verfahren besser allerdings ist der Rechenaufwand durch die Lösung des Gleichungssystems aufwändiger.
Ist die rechte Seite nichtlinear, dann muss die Lösung mit einem iterativen Verfahren bestimmt werden
(Stabilität bestimmt die Schrittweite, also wie groß unser $\Delta t$ ist)
Vergleich der Stabilitätsgebiete verschiedener Zeitintegrationsverfahren
Wie groß darf $\Delta t$ sein, dass das Verfahren Stabil bleibt? (Stabilität gleichzusetzen mit Abstand zwischen Numerischer und wirklicher Lösung bleibt möglichst Gleich, es ist nicht gleichzusetzen mit Genauigkeit)
Je genauer das Integrationsverfahren, desto größere Zeitschritte können gewählt werden
Einschritt-Verfahren: Runge-Kutta-Verfahren
EInschrittverfahren, es kommt nur $t_n$ und $t_{n+1}$ vor, es werden zwischenschritte genutzt
"Absolutes Standartverfahren"
Mehrschritt-Verfahren: Adams Bashforth-Verfahren (explizit) / Adams Moulton-Verfahren (implizit)
Vorteil implizite Verfahren:
- Neue Lösung ist bereits in Approximations Gleichung eingebaut
- Zeitschrittintervall kann viel Größer sein
Vorteil explizite Verfahren:
- Leichter zu programmieren
- Kleine Zeitschrittintervalle (Eigentlich kein Vorteil)
Fazit: Zeitapproximation
- Explizite Verfahren Rechenaufwand pro Zeitschritt klein\
- Allerdings Zeitschrittweitenbedingung wegen der Stabilität, Implizite Verfahren haben diese Restriktion nicht
- Wenn der Zeitschritt deutlich größer sein könnte, als durch die explizite Stabilitätsbedingung vorgegeben, dann implizites Verfahren
- Impliziten Verfahren Rechenaufwand pro Zeitschritt höher, man kann
- Unter Umständen sehr große Zeitschritte wählbar
Das Differenzenverfahren
- Diskretisierung des Rechengebiets in Punkte $x_i$
- Auswahl und Einsetzen der Differenzenquotienten
- Sortieren der Differenzengleichungen
- Lösen des Gleichungssystems