Analytische und Numerische Methoden - Numerik

24 April 2025, Andrea Beck

Approximation im quadratischen Mittel

$$...$$

Numerische Differentiation und Integration 4.2

Die numerische Differenziation und Integration kann jetzt durchgeführt werden, indem die btrachtete Funktion durch ein Interpolationspolynom approximiert wird und dieses dann abgeleitet oder integriert wird Dadurch, dass Polynome hohen Grades gerne oszillieren, unterteilt man bei der numerischen integration mit dem Newton-Cotes-Verfahren mit einer Zerlegung des Integrationsintervalls in Teilintervalle kombiniert. Man spricht dann von der aufsummierten Newton-Cotes_Formel

Eine bessere Wahl der Stützstellen führt auf die Gauß-Quadratur-Formeln. Hier sind die Stützstellen durch die Gaußpunkte gegeben.

Numerische Integration

Gesucht ist eine Approximation des bestimmten Integrals einer Funktion $f$

$$Q = \int_a^b f(x) dx$$

Ersetzt man den Integranden f durch ein Polynom und integriert das Polynom erhält man eine greichtete Mittelwertsformel

$$Q_h = \sum_{i=0}^N a_i f(x_i)$$

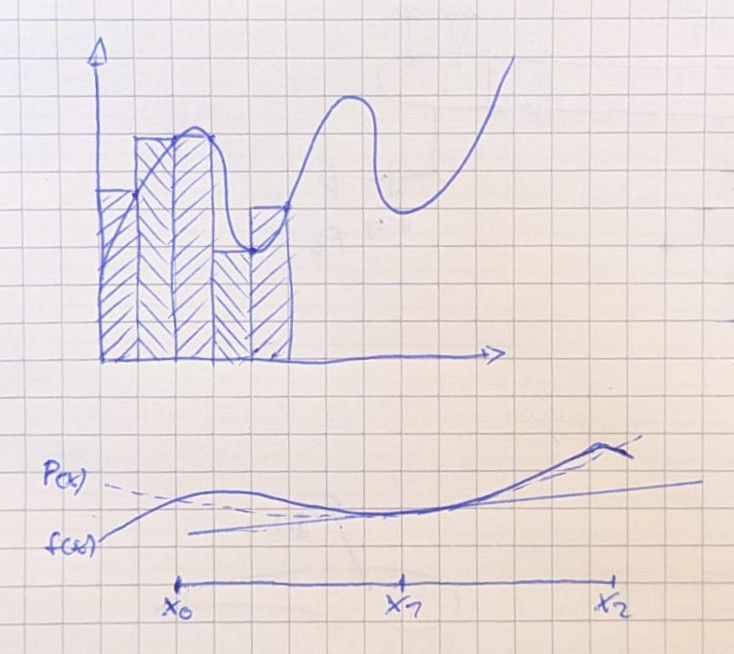
Wird die Anzahl der Rechtecke verzehnfacht, wird der Fehler um das zehnfache reduziert
Fehler verhält sich li near zur Anzahl der Stützstellen, Experimentelle Konvergenzordnung (EOC) = 1

Andere Approximationsmethoden haben ein anderes verhalten, zum Beispiel Mittelpunktregel mit EOC = 2

Gauß-Quadratur

$$Q_h = \sum_{i=0}^N a_i f(x_i)$$

$$...$$

Sowohl die Gewichte $a_i$ als auch die Stützstellen $x_i$ werden so bestommt, dass die Genauigkeit möglichst groß ist - nicht äquidistante Stützstellen

Optimalste Quadratur - mit weniger Stützstellen erreicht sie eine gleiche oder höhere Genauigkeit als die Newton-Cotes-Formel

• Die Gauß-Punkte sind immer im Intervall $[1,-1]$ angegeben
• Ablesbar aus Tabelle, muss nicht jedes Mal aufs neue berechnet werden

Numerische Differentiation

Gesucht ist eine Approximation der Ableitung der Funktion

$$y = f(x) \quad für \quad x \in [a,b]$$

$$...$$

Exakte Ableitung von p(x) wird als Approximation der Ableitung von f(x) an der Stelle x genutzt
Einfacherer Fall: Äquidistante Stützstellen

Bestimmung des Approximationsfehlers:

$$...$$

Tabelle: Zentrale Differenzenquotienten (Folie 30)

Ableitung am Punkt 0, weitere Spalten sind Indexe der umgebenden Gitterpunkte, eins neben 0 ist z.B $\pm$ 1\

Ist z.B. eine Zweite Ableitung gesucht, steht diese im Zweiten Block - Zeilen innerhalb des Blocks werden so gelesen:
Koeffizienten der Werte an den entsprechenden Stellen
Restterm ist der Fehler, der durch Ersetzung der ursprünglichen Kontinuierlichen Funktion mit der Approximierten Funktion entsteht - Kovergenzordnung des Verfahrens kann am Exponenten von $h$ im Restterm abgelesen werden - Ist in der Klausur meist Ausschlaggebend für welche Zeile genau gewählt werden soll.

Fazit

Äquidistante Verteilung der Stützstellen ist einfach...

Iterative Lösungen von nichtlinearen Gleichungen

Nichtlineares Gleichungssystem der Form

$$\underline{F}(\underline{u}) = 0$$

Fixpunktgleichung führt auf eine Iterationsvorschrift.
Das Iterationsverfahren konvergiert, wenn die Funktion $G$ eine Kontraktion ist.Im skalaren Fall einer einzelnen Gleichung kann man dies bei einer stetig differenzierbaren Funktion $G$ nachweisen, indem man zeigt, dass die Ungleichung

$$|\frac{\partial G(u)}{\partial u}| < 1$$

für alle $u$ erfüllt ist.