Analytische und Numerische Methoden - Numerik
22 April 2025, Andrea Beck
Kapitel 4
Übersicht über grundlegende Methoden der Numerik:
- Approximation und Interpolation
- numerische Intragration und Differentiation
- Iterationsverfahren
- Iterative Lösungen von linearen Gleichungssystemen
- numerische Lösungen von Eigenwertproblemen
Approximation bedeutet: Man sucht eine (einfachere) Funktion $p = p(x), x$ aus $[a,b]$, welche die gegebene Funktion $f = f(x), x$ aus $[a,b]$ möglichst gut approximiert\
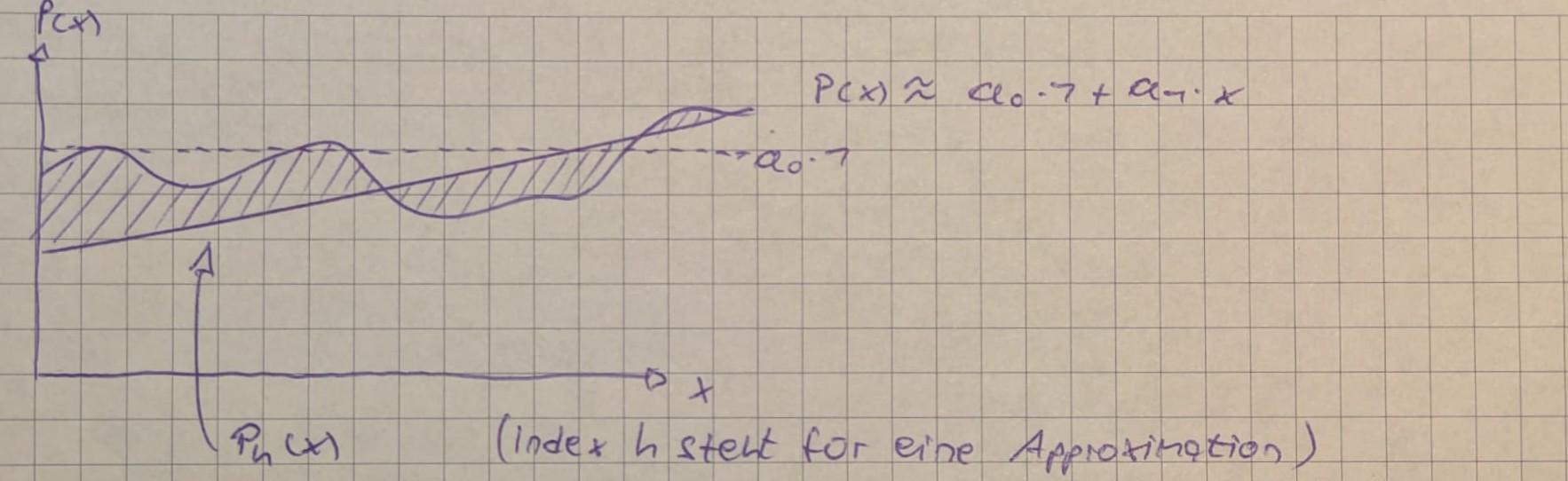
Wir brauchen ein Maß dafür, wie gut eine Approximation die tazächliche Funktion Annährt
möglichst gut könnte bedeuten, bezüglich einer Norm:
$$||p(x) - f(x)|| = minimal$$
Zum Beispiel möglichst gut im quadratischen Mittel (Siehe markierte Fläche in der Skizze):
$$||p(x) - f(x)||_2 = \frac{1}{b-a} \sqrt{\int_a^b(p(x)-f(x))^2dx}$$
oder auch möglichst gut bezüglich dem maximalen Abstand (Folien Seite 5):
$$||p(x) - f(x)||_\inf = ...$$

Kollokation: beschreibt, dass wir zwei Dinge an einem Punkt gleichsetzen (Überbegriff)
Interpolation: Spezieller Name des Annährungsverfahrens über eine Interpolationsfunktion
Wahl der Basisfunktionen
Darstellung eines Interpolationspolynoms
- Mit Hilfe der Monombasis
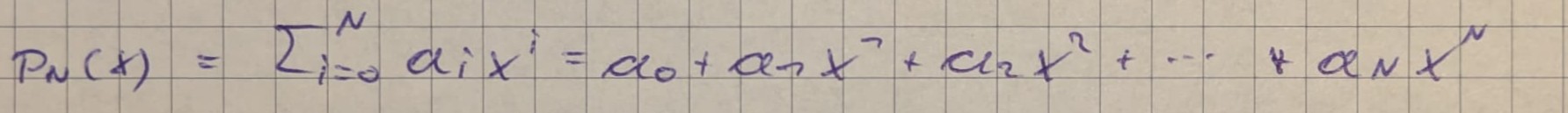
- Lagrange Darstellung
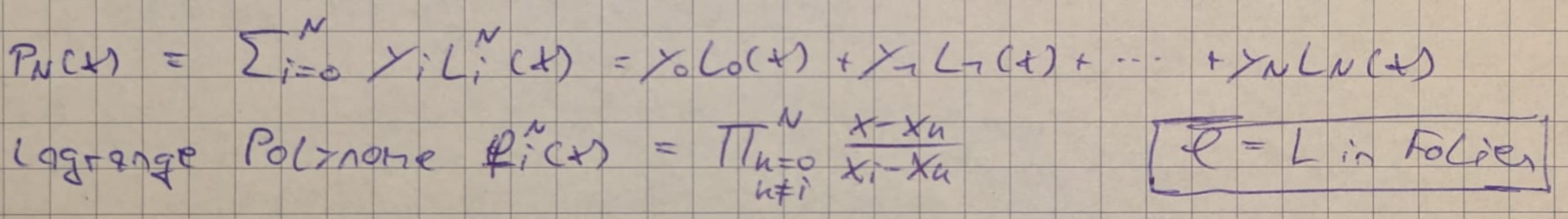
Werden auch Lagrangesche Basis-Polynome genannt
Definiert durch die Vorgabe der Punkte $x_i$
- Newtonsche Darstellung

Prüfungsähnliche Frage Beispiel 4.2 Folie 12
Die Güte des Interpolationspolynoms und dessen Stabilität hängt von der Wahl der Stützstellen ab. Punkteverteilungen, bei denen die Interpolationspunkte sich am Rand verdichten, bessern die Approximation, z.B. die Gaußpunkte oder die Chebyshev-Punkte (Siehe Folie 14)
$$x_i = \frac{a+b}{2} - \frac{b-a}{2} cos(\frac{i \pi}{N})$$
Alternative: Äquidistante Stützstellen - aber mit stückweisen Polynomen: Splines
Stückweise kubische Polynome, die weniger oder fast nicht schwingen
Fazit: Approximation durch Interpolationspolynome
-
Äquidistante Verteilung die Stützstellen ist einfacher aber ungünstig: Oszillationen vor allem am Rand
-
Wenn, dann Polynome niederen Grades
-
Besser: Punktemengen, welche sich am Rand häufen
-
Besser, bzw. stabiler: Statt Polynome höheren Grades stückweise Polynome niederen Grades
-
Kollokation sind lokale Bedingungen
-
Besser: Minimierung bzgl. einer Norm - Integralen Bedingungen